MULTIPRODUCT OPERATIONS—2 (Conclusion): New scheduling rule improves pipeline efficiency

Vanina Cafaro,
Diego C. Cafaro,
Carlos A. Mendez,
Jaime Cerda
INTEC (UNL-CONICET)
Sante Fe, Argentina

A new rule prioritizing product delivery to the eligible terminal closest to the one being currently served reduces total accumulated idle volume by about 40% and decreases the number of cut operations.

Different priority arrays lead to different delivery schedules, strongly affecting cost-efficiency of the solution achieved. Prioritizing nearest-to-refinery terminals, for instance, may reduce the total volume of segments stopped, but the number of stripping operations will surely increase. Prioritizing the farthest terminals, however, may increase the number and volume of pipeline stoppages.

Part 1 of this series (OGJ, Aug. 1, 2011, p. 98) discussed development of the discrete event simulation system on "Arena." This concluding second part applies the system to management of a real-world products pipeline with a single input and multiple delivery points.

The approach described allows use of emerging simulation-based optimization tools to improve performance of the resulting schedules. Future work will focus on developing efficient priority rules combined with heuristic search and rigorous formulations to find cost-efficient and robust solutions for detailed scheduling of multiproduct pipeline networks with different configurations.

Input station

The input station lies at the origin of the pipeline system. Product batches discharged from input tanks enter the line while production runs from the neighboring refineries are being loaded. Storage tanks and pumps make up the input station, and the simulation system forces pipeline activity to stop when available stock is running out.

Different components model operations at the input station. Production schedule is the first component. New products arrivals (production runs) discharge into storage tanks at pre-defined times.

Modeling the inventory level in every storage tank as a continuous variable allows accurate control of product stocks at the input station. Since handling product batches occurs discretely, their volumes are expressed as small, equal-size batch elements called entities. Each entity represents a specific volume of a certain product. If the entity size decreases, a larger number of batch elements will be required, and a more accurate model will be achieved. Choosing a proper entity volume is therefore a major decision.

The second operational module of the input station is the input schedule. A given program shows the sequence of batches to be injected into the line and the batch attributes, i.e., product type, volume, mean pump rate, and start pumping time. Entity attributes are inherited from the batch to which the entity belongs.

A final key decision is the pump rate at which batch elements are injected. Design and operational constraints should be considered. Pressure limits must be respected, and turbulent flow should be maintained to minimize product interface volumes.

A major component of transportation cost is the energy consumed moving product batches into the line. The pump rate of the batches strongly affects the pumping cost, placing a premium on the proposed simulation model's ability accurately to choose different pump rates for different batch parts or entities of a real pipeline system.

Oil pipeline operators should also avoid running pump stations at daily peak periods because a much higher price must be paid for electricity. The pipeline simulation system easily accounts for high pumping-cost intervals.

Pipes

The pipeline system, divided into different segments (pipes), connects the nodes of the distribution network. Each pipe, modeled as a fixed-size first-in/first-out (FIFO) queue with a single server at the pipe extreme, permits the movement of material entities from one position to another. By combining different pipes, with particular sizes and service rates, the model simulates the operation of almost every pipeline system structure.

Every time an entity enters a pipeline segment at the inlet point, it pushes the entity positioned at the other extreme out of the queue. A server at every pipe end dispatches the first entity on the queue whenever a new entity enters the pipe at the inlet section. Since the system transports multiple products, the model keeps track of every pipe linefill by updating the server queues at every time event.

The actions a pipe server can take on the entity waiting for service are:

• No action.

• Movement to the next pipe.

• Loading in a terminal tank.

The beginning of the scheduling horizon requires creating the pipeline contents' initial conditions using the initialization process. The number of entities each pipe holds determines its volume. This number remains constant across the scheduling horizon as the volume of each pipe is a fixed quantity given by cross section and segment length.

Terminals

Terminals are tank-farms from which products are sent to consumer markets. In the proposed simulation model, arrivals of product entities from the line and deliveries to regional markets occur simultaneously.

The tanks have a maximum capacity that cannot be exceeded and, in general, a minimum level of material is also required to maintain normal operations. Continuous variables model the inventory level in storage tanks.

The simulation model automatically generates the pipeline output schedule according to the requirements of each terminal. The terminal-batch assignment matrix (Q_k^o(i,j)) from the optimization module provides terminal requirements.

Product batches, on the other hand, travel to local markets from terminal tanks mainly by truck. Delivery due-dates and tank discharge rates provide the basis for continuously updated market demands, making it possible to define daily or hourly demand patterns. Empirical-probabilistic distributions can also represent stochastic demands.

Priority rules

When a product batch entity reaches the terminal that demands it, the entity may be transferred from the pipeline to an available terminal tank. At every pumping event, only one terminal can receive a single product unit from the pipeline. Every entity between the input station and the selected terminal moves, while the rest of the pipeline remains idle.

To decide which of the eligible servers should dispatch the first entity on its queue to the associated terminal, the simulation model applies alternative heuristic rules assigning different priorities to terminals, choosing the one that should receive demanded products first. Applying three priority rules solves the case study introduced in the next section:

• The Nearest-First (NF) rule prioritizes product delivery to the eligible terminal closest to the origin. If two alternative terminals are able to receive a product unit, NF selects the one positioned closer to the beginning of the line. No required product will overpass a demanding terminal since upstream locations are always prioritized.

• The Farthest-First (FF) rule prioritizes product deliveries to the farthest eligible terminal from the origin, requiring verification that the delivery of an entity to the prioritized terminal does not prevent satisfaction of upstream product demand.

In a unidirectional pipeline, such as considered here, an entity that overpasses a terminal cannot be transferred to it. If such an entity is absolutely necessary to meet a depot's demand, the resulting output schedule would be infeasible. Making terminal Tj "restrictive" prevents any other eligible terminal farther from the origin being the selected destination, and only terminals T1 to Tj can receive a product entity.

• The Nearest-to-Current terminal (NC) rule prioritizes product delivery to the eligible terminal closest to the one currently being served. If two alternative terminals are able to receive a product unit, it selects the one closer to the terminal being served. The current terminal would obviously have highest priority.

Prioritizing the nearest-to-current terminal allows simultaneously reducing both the total volume of idle pipeline segments and the number of stripping operations (turning on-off pump stations).

Using different priority rules, the logic structure of the model generates alternative delivery schedules considering the current state of the pipeline (product availability and batch location) and depot requirements. The sequence of transfers of material entities from the pipes to receiving terminals over time determines the delivery schedule.

Case study

Application of the proposed simulation-based model to a real-world problem^1-3 focused on daily operation of a pipeline, transporting from a main refinery to multiple depots. The 955-km system transports four refined products (gasoline, diesel, LPG, and jet-fuel) to five distribution terminals.

The applied model makes use of the monthly input schedule generated by the optimization module.³ Transported material consists of relatively small entities (100 cu m), requiring a total of 1,635 entities to fill the whole line.

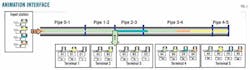
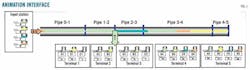
Animated interface

Fig. 1 shows the simulation-based interface developed on the Arena simulation package. The animated interface allows visualization of pipeline operations, showing the dynamic evolution of the pipeline network state over time. The software also permits development of graphic representations to assess real-time operation.