FRACTURE PROPAGATION—1: Fracture-arrest prediction requires correction factors

As σ increases, the required CVN energy increases by the power of 1.5 to 2 on σ. And, since the hoop stress is the product of the design factor and the SMYS, as the design stress and SMYS increase, the required CVN for arrest also increases.

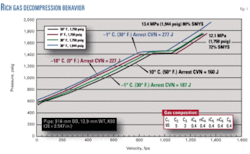
• Pressure, temperature. Pressure and temperature of the gas, especially for rich gas, determine the starting conditions, for the gas’ decompression and affect the pressure where the gas enters the two-phase region. shows examples of gas decompression curves for the same gas composition decompressing from two different pressure levels.

Gasdecom, based on the BWRS equation of state, predicted the curves shown.¹ The 12.1 MPa (1,750 psig), –1° C. (30° F.), and 10° C. (50° F.) curves start decompressing from about the same velocity, but the –18° C. (0° F.) curve has a higher initial velocity.

The level of pressure decay in the bottom portion of the decay after the gas has penetrated into the two-phase region stands as the important feature of the three curves. The lowest-temperature curves on the 1,750 psig (12.1 MPa) plot have the highest pressures available to drive a fracture. Comparing the 1,944 and 1,750 psig curves at -1° C. (30° F.) shows the higher-pressure curve having a higher pressure in the lower portion of the decay, as would be expected.

These curves provide an example of the sensitivity of gas decompression to starting temperature and pressure and how it affects the fracture toughness required for fracture arrest. Predicting fracture-arrest toughness with the Battelle Two Curve Model (TCM)1 shows the higher the pressure the greater the fracture toughness required for arrest.

The CVN arrest toughnesses predicted for arrest (with no correction factor) are:

• 277 J for the 13.4 MPa, –1° C. curve.
• 227 J for the 12.1 MPa, –18° C. curve.
• 187 J for the 12.1 MPa, –1° C. curve.
• 160 J for the 12.1 MPa, 10° C. curve.

Arrest toughness is sensitive to the initial temperature and pressure in a pipeline.

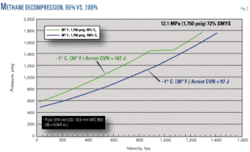
• Gas composition. Gas composition also affects gas decompression. Fig. 2 shows two gas compositions, one the same composition shown in Fig. 1 and the other 100% methane (C₁), decompressing from the same pressure and temperature (12.1 MPa, –1° C.), demonstrating the richer the gas the higher the pressure driving the fracture and the greater the toughness (187 J vs. 97 J) required for fracture arrest.

An attempt to assess the effect of composition changes for all of the individual elements in natural gas sought to develop a relative ranking of the significance of the composition effect on the fracture-arrest toughness. Examination of the effort, however, proved it to be impossible.

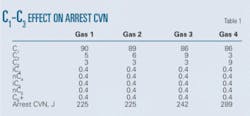
Tables 1 and 2 show examples of the assessments. Table 1 shows an attempt to assess the effect of C₁, C₂, and C₃ on the arrest CVN for the gas examined in Fig. 1 at 12.1 MPa (1,750 psig) and 10° C. (50° F.).

Comparing Gas 1 and 2, the decrease of C₁ to 89% from 90% and increase of C₂ to 6% from 5% did not change the arrest CVN, suggesting 1% of C₁ and C₂ have an equal effect on arrest toughness. Comparing Gas 2 and 3, however, shows decreasing methane to 86% from 89% and increasing ethane to 9% from 6%, keeping all other factors constant, increased the arrest toughness to 242 J from 225 J, illustrating the non-linear effect of the composition. Holding C₁ constant at 86% but decreasing C₂ to 3% from 9% and increasing C₃ to 9% from 3% increased the arrest toughness to 289 J from 242 J.

Table 2 shows the effect of changing C₄, C₅, and C₆ compositions. C₁, C₂, and C₃ stayed constant, along with pressure and temperature. Normal levels of C₄ through C₆ are usually less than 0.2%, but even changing the amounts to 0.4% did not affect arrest toughness, with CVN values of 220-222 J.

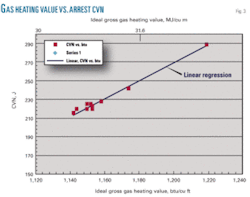
A second attempt to find an approximate predictor for the arrest toughness based on composition used the ideal gas heating value shown in Fig. 3. Equation 2 provides the basis of the gas heating value.

Fig. 3 shows a roughly linear relationship between the ideal gas heating value and the arrest CVN energy, providing perhaps one of the best ways of assessing a given gas composition’s effect on fracture-arrest energy. This approach needs further examination, but appears promising.

Surrounding material

The type of backfill material (backfill) above and below the pipe, i.e., air, soil, or water, affects the required fracture toughness for arrest. Rudland and Wilkowski reported the results of research studying the effect of soil properties on fracture speed.² The correlation in results of their small-scale fracture propagation tests, plotting fracture speed vs. soil density, suggests a trend of fracture speed being lower for higher density soils, but it is rough at best and needs additional study.

Plotting fracture speed against moisture content shows a clear trend toward decreasing fracture speed with increasing moisture content. The effect of moisture content (as opposed to soil type), however, is not clear as to whether the increase in density or some other parameter is responsible. Plotting different soil types with the same moisture content would help clarify its role. The data reinforce the need to study the effect of different soil types, depths of soil, moisture contents, and density to help reduce scatter in future full-scale fracture-arrest tests.

A pipe submerged underwater to sufficient depth will arrest a fracture at a lower CVN level than a similar fracture backfilled with soil. Maxey postulated releasing gas into the water creates an external pressure on the pipe reducing the effective driving pressure in the pipe.³ Water transmits the exiting gas pressure at a velocity of 1,463 m/sec (4,800 fps), 3.7 times faster than the gas pressure in the pipe can decay, roughly 396 m/sec. The water has sufficient mass to restrain temporarily the exiting gas pressure, allowing it to apply external pressure on the pipe for a long enough time to assist in fracture arrest.

No existing fracture-arrest prediction method used to specify CVN fracture-arrest toughness has incorporated the effect of backfill in a way allowing variations to be effective on the calculated arrest toughness. This area needs additional research to accurately predict arrest toughness levels and, one hopes, reduce scatter in future correlations with full-scale fracture-arrest tests.

X70 predictions

Most formulations for prediction of fracture-arrest toughness emerged 1970-90 and are generally based on X52-X65 grade pipe steels. These steels characteristically had relatively low constant upper plateau energy levels and most were relatively thin (6-12 mm), prompting use of two-thirds thickness CVN specimens to measure toughness of the steels and develop arrest-prediction models for fracture toughness assessments.

Newer steels, X70-X100, used at higher operating pressures, 10.3-34.5 MPa (1,500 to 5,000 psig), have sufficient WT to allow use of full-thickness CVN specimens for fracture toughness assessment. Some of the X70 and X80 steels also exhibited rising upper shelf energies and the interpretation of the arrest toughness for these steels using CVN specimens has not been defined.

This portion of the article will present raw data from full-scale burst fracture-arrest tests on X70 pipe, sorting the data by where arrest or propagation occurred and assessing it against available prediction methodologies.

The X70 data consist of tests involving both lean gas and rich gas. The rich-gas tests showed discontinuity in the decompression curve, while the lean-gas tests exhibited a continuous decompression curve.

The X70 lean gas full-scale fracture arrest data come from 12 tests encompassing 101 data points on individual pipe lengths (Table 3). The tests cover 42-56 in. OD and 15.7-20 mm WT. The Battelle TCM provided the basis for all of the predicted fracture-arrest toughness values.2

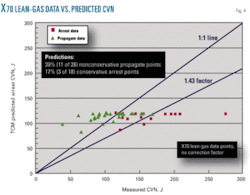
Fig. 4 shows the X70 lean gas fracture-arrest data. Measured CVN values from the test pipe lie on the X axis and the TCM-predicted arrest CVN values on the Y axis. Thirty-nine percent of the propagate data lie on the right side of the 1:1 line, which are nonconservative propagate points. Seventeen percent of the arrest data lie on the left side of the 1:1 line, which are conservative arrest points.

The TCM predictions are too low to match the test results. Eliminating all the nonconservative propagate points, i.e., moving them above the 1:1 line, would require a 43% increase in the predictions or use of 1.43 multiplier factor.

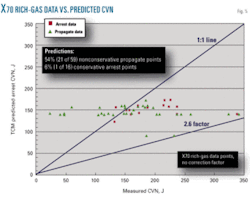
Fig. 5 shows similar data from rich gas tests on X70 pipe (Table 4), representing nine fracture-arrest tests with 75 individual pipe lengths.

Fig. 5 shows 54% of the propagate data on the right side of the 1:1 line (nonconservative) and 6% of the arrest data on the left side of the 1:1 line (conservative). TCM predictions are even further in error for the X70 rich-gas test results. Eliminating the nonconservative propagate points would require applying a 2.6 multiplier factor to the predicted toughness levels, raising a question as to why such a stark difference between the lean-gas and rich-gas data points exists.

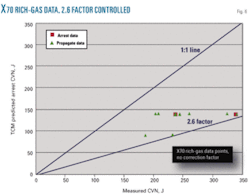
Examination of the data revealed one outlying rich gas data set as controlling the 2.6 factor. These data, shown in Fig. 6, represent tests conducted in the 1980s with results well outside the scatter of the other data points. These tests could have used rising upper shelf CVN energy steels, the type of X70 steel produced at the time, but this is speculation. A lack of knowledge regarding how to assess the toughness of rising upper shelf steel CVN energies requires full-scale tests to define their fracture-arrest characteristics.

Removing the earlier data shown in Fig. 6 from Fig. 5 reduces the 2.6 factor to the 1.43 shown in Fig. 4.

Three correction equations have been proposed to eliminate the error identified in Figs. 4 and 5. Equation 3 shows the Leis correction equation.

Wilkowski developed another equation (Equation 4), using the same terms used in Equation 2.

CFER proposed the third correction factor of 1.7 times the CVN TCM prediction.⁴

Equation 3 appears to provide the most reasonable approach for X70 steels. This is also suggested for application to high CVN-energy (>70 ft-lb) X65 steels.

References

1. Eiber, R.J., Bubenik, T.A., and Maxey, W.A., “Fracture Control Technology for Natural Gas Pipeline,” Report NG-18, No. 206, PRCI Catalog No. L51691, December 1993.
2. Rudland, D., and Wilkowski, G., “The Effects of Soil Properties on the Fracture Speeds of Propagating Axial Crack in Line Pipe Steels,” Paper No. 10086, International Pipeline Conference, Alberta, Sept. 25-29, 2006.
3. Maxey, W.A., “Experimental Evaluation of Fracture Propagation in an Underwater Gas Pipeline,” PRCI Catalog No. L51470, June 3, 1985.
4. Wolodko, J., and Stephens, M., “Applicability of Existing Models for Predicting Ductile Fracture Arrest in High Pressure Pipelines,” Paper No. 10110, International Pipeline Conference, Alberta, Sept. 25-29, 2006.

The author

Bob Eiber ([email protected]) is president of Robert J. Eiber Consultant Inc. in Columbus, Ohio. He has served on the ASME B31.8 committee, API Line Pipe committee, and was chairman of the ASTM (ISO) committee preparing a DWTT Standard for ISO. He was the director of pipeline transmission research at Battelle when he retired. He holds BS and MS degrees from Case Western Reserve University and is a member of ASME and ASTM.