Pipeline repairs require fewer layers using aramid fibers

Mourad Bettayeb
Noureddine Abdelbaki
Mohamed Gaceb
Université M’Hamed Bougara de Boumerdes
Bourmerdes, Algeria

First-order reliability methods (FORM) of structural reliability assessment allowed optimization of the thicknesses of fiberglass reinforced polyester (FRP) resin necessary for pipeline repair using a composite material repair technique and discerned that aramid fibers require less material. A probabilistic approach allowed consideration of the random nature of the mechanical characteristics of materials used and the uncertainties of the results of on-line diagnosis when studying the resistance of line pipe reinforced by two types of composite materials based on fiberglass and aramid fibers. To check the strength and effectiveness of this type of repair, several methods and standards were used, with some conservatism in estimating the failure pressure and the thicknesses required for the repair.

Reliability calculation

Formulation of the failure criterion by a limit state function depends on a set of random basic variables X=(x1,x2,…xn). In n-dimensional space, it separates the physical security field from the admissible situations defined by g(X) > 0, from those that are not, defined by g(X) < 0, in the failure domain. For the case of structural elements, this function is given for the elementary stress-strength case (Equation 1).¹

The border is the limit-state surface or the performance function. If the joint density function is known, the probability of failure Pf can be defined by Equations 2.

Pf can be calculated by the FORM method, based on the reliability-index calculation. Its implementation is based on the following steps:

The transformation of basic variables xi into reduced normal-centered statically independent random variables, ui. The space of the basic variables (including the limit-state function) is transformed into a standard normal space. This transformation is called isoprobabilistic transformation and noted by Equation 3.
In the standard space of the ui variables, the objective is to determine the design point of the limit-state surface, P* = (u1*... un*), which is the closest point to the origin. It corresponds to the Hasofer-Lind reliability index βHL, and is the most probable failure point, whose coordinates define the combination of variables most likely to cause failure. The problem is therefore reduced to finding the minimum value of the distance OP* given by Equation 4. This becomes an optimization problem, where a search process is necessary and an iterative algorithm is used in determining a minimized distance (Equation 5).
The limit State surface g (U) = 0 expressed in the new space is approached by its tangent hyperplane at the design point P*. The probability of failure is then given by Equation 6.

Mechanical formulation

Mechanical formulation begins by determining the limit-state function, which represents the pipe failure criterion. It is written as shown in Equation 7, in which P0 is the service pressure and PD the failure pressure of the pipe, given by Equations 8-9 and 11-12 for various circumstances.

Case 1 – Pipe without corrosion. PD for intact pipe is given by B31G (Equation 8).²
Case 2 – Non-repaired corroded pipe, using modified B 31G standard (Equations 9-10) (OGJ, Aug. 20, 1990, pp. 56-59).
Case 3 – Non-repaired corroded pipe, using SHELL 92 standard (Equation 11).³
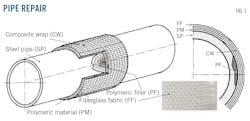
Case 4 – Corroded pipe, repaired using composite material in the presence of an external corrosion defect with internal pressure alone, where the mechanical model shown in Equations 12-14 is used (Fig. 1).⁴

Case study

The Level 2 FORM was used to evaluate failure probability Pf and reliability index β, applying a MATLAB program already used in previous reliability studies to conduct calculations (Oil & Gas Journal, Jan. 5, 2015, pp. 80-85). The iterative minimization algorithm HL-RF was used in the reduced standard normal space for the determination of the design point of the limit-state surface.

As part of this study, a reliability calculation by probabilistic approach was made on a 45-km section of 26-in. OD pipeline made of API 5L X52 steel and subjected to internal pressure alone. The calculation was done first on an intact pipe, then on a pipe in the presence of external corrosion defects without rehabilitation in the second and third cases, and lastly on a rehabilitated pipe. Table 1 provides data from this study.

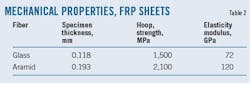
Table 2 shows the different characteristics of the composite materials used (which are unidirectional based on fiberglass and aramid fibers oriented in the circumferential direction} for the pipeline rehabilitated using composite materials. Normal distribution was chosen for the limit of the circumferential strength with a coefficient of variation Cov = 0.05.

Results

A first calculation of the failure probability Pf used the method of approximation FORM for an intact pipe and a pipe with corrosion defects with different depths ranging from 10-70% of the nominal thickness of the pipe and for different service pressures P0, based on the Modified B31G and Shell 92 standards (Fig. 2).

The failure probability Pf increases with increased service pressure for all the corrosion defect depths under study. For the same value of service pressure, the variance of the failure probability between shallow defects and very deep defects is more important for small service pressures than for large service pressures. This difference decreases with the increase of the service pressure and tends to cancel when the pressure reaches a value at which no defect is tolerated and the failure probability tends towards 1.

In all calculation cases, the failure probabilities calculated by the Shell 92 standard are greater than those calculated by the Modified B31G standard where the deviation of the probability of failure decreases with increase in the service pressure for all depths of corrosion defects. The probabilities of failure of the pipe without defect (intact pipe) are closer to the values found by the Shell 92 standard than those of the Modified B31G standard for depths of 10% WT.

If a target of Pf = 1.10-3 is chosen to avoid any serious consequences caused by the failure of this type of structure, corrosion defects of more than 70% depth are not tolerated for any service pressure according to both standards. The smallest defects of 10% depth allow a pressure of 7 MPa and 6.5 MPa according to the modified B31G and the Shell 92, respectively.

To ensure the safety of these pipes several defects require repair, according to the terms of reliability or probability of failure in the study.

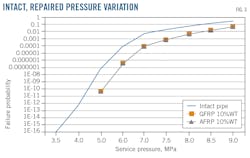
A second calculation of the probabilities of failure was carried out for pipes rehabilitated using composite materials based on fiberglass (GFRP) and Aramid (AFRP) fibers (Fig. 3). The cases of calculation of the smallest defects (10% WT) and deeper defects (70% WT) are givens.

At the same time, however, the curves of the pipes repaired by GFRP and AFRP are mixed for all corrosion defect depths in terms of probability of failure. The same for both types of composite materials for the repaired pipe. The probability of failure for the smallest service pressures below 5 MPa is zero, because there is no risk of rupture. The maximum service pressure for the same target of Pf = 1.10-3 is Po = 6.5 MPa for the flawless pipe and Po = 7.6 MPa for all repaired pipes.

As there is no difference between the results found for the two types of composite materials used for rehabilitation in terms of probability of failure, the variation in the thickness of the composite material required for repair was considered for different depths of defects studied in terms of service pressure (Fig. 4). These thicknesses were calculated at the design point P* mentioned earlier (Equation 5), taking into account the different random variables used, yielding an optimization of the thicknesses of composites necessary for the repair.

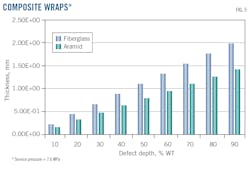
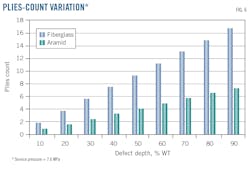
There is an increase in the thickness with the increase in the service pressure for all depths of defect. This increase is particularly important as the defects near 90% WT.

For the same depth of defect, the increase in composite thickness with increase in service pressure is much greater for fiberglass material. For the same service pressure, required composite thickness is greater for fiberglass than for aramid fiber materials.

This difference is very significant for deep corrosion defects, for which variation between the minimum thicknesses of WTGFRP and WTAFRP corresponding to a pressure P0 = 3 MPa for 90% WT defects is almost ten-fold that for 10% WT defects. The same thing is observed for the variation between the minimum thicknesses corresponding to service pressure P0 = 9 MPa (Fig. 6).

Using the same target value of Pf (1.10-3), the corresponding maximum service pressure is P0 = 7.6 MPa for all rehabilitated corroded pipes (Fig. 3). For this same maximum value of service pressure, calculations were made for both types of composite materials of the thicknesses necessary for the repair (Fig. 5) and the number of useful plies (Fig. 6) for different depths of corrosion defects. There is a growth in the thickness required for repair with the increase in the depth of corrosion defects. The thicknesses of fiberglass-based composite materials, however, remain greater than those of aramid fiber-based composite materials.

This difference in thickness is increasingly important as the defects become deeper, progressing from 17 plies from 2 for GFRP and to 8 plies from 1 for AFRP, for depths of 90% and 10% respectively.

Overall, the probability of failures found were similar for all pipes repaired by the two types of composite materials and was close to that of uncorroded pipe. It was not clear though that composite materials based on aramid fibers provide a better performance than fiberglass-based materials in improving the ultimate internal pressure capacity of pipes. This can, however, be seen in the curve of the variation in the thickness of these materials as a function of service pressure used and repaired corrosion defect depths, in which the fiberglass-based material always required a greater thickness than the aramid fibers.

References

Lemaire, M., Chateauneuf, A., and Mitteau, J.C., « Fiabilité des structures : couplage mécano-fiabiliste statique,” Hermès Science Publications, Paris, 2005.
Teixeira, A.P., Guedes Soares, C., Netto, T.A., and Estefen, S.F., “Reliability of pipelines with corrosion defects,” International Journal of Pressure Vessels and Piping, Vol. 85, No. 4, April 2008, pp. 228-237.
Cosham, A., Hopkins, P., Macdonald, K.A., “Best practice for the assessment of defects in pipelines - Corrosion,” Engineering Failure Analysis, Vol. 14, No. 7, October 2007, pp. 1245–1265.
Alexander, C. and Francini, B., “State of the art assessment of composite systems used to repair transmission pipelines,” International Pipeline Conference, Calgary, Sept. 25-29, 2006.

The authors

Mourad Bettayeb ([email protected]) is lecturer at Université M’Hamed Bougara de Boumerdes, faculty of hydrocarbons and chemistry, Boumerdes, Algeria. He holds a graduate degree in aeronautic engineering from the University of Blida (1995), a European diploma in applied science in advanced solid mechanics and structures calculation (2001) from University of Liege, Belgium, and a PhD (2016) from University of Boumerdes.

Nouredine Abdelbaki ([email protected]) is professor at Université M’Hamed Bougara de Boumerdes. He has also served as dean of oil and chemistry faculty, director of the Laboratory of Reliability of Hydrocarbon Equipment and Materials at University of Boumerdes, and vice rector at University of Bouira. He holds a graduate degree in hydrocarbon engineering (1982) from the University of Boumerdès and a PhD (1988) from University of Oil and Gas in Moscow, Russia.

Mohamed Gaceb ([email protected]) is Professor at Université M’Hamed Bougara de Boumerdes. He has also served as a head of the department and cirector of a research laboratory at the same university and head of the fracture mechanics subdivision at the Research Centre for Energy Conversion Systems in Algiers, and as a senior lecturer at the University of Blida. He holds a graduate degree in mechanical engineering from the University of Sheffield, UK (1980) and a PhD (1985) from Sheffield Hallam University.