Downhole temperature, pressure methods are accurate for drilling, completion, cement design
Accurate prediction of bottomhole circulating temperature is important during drilling and completion of oil and gas wells and critical for properly designed cement slurries.
Downhole temperature is an important factor affecting cement thickening time, rheological properties, compressive strength development, and set time. Researchers have developed methods to allow the industry to determine downhole mud temperatures and hydrostatic pressures accurately.
The American Petroleum Institute (API) Subcommittee 10 for well cements has developed new temperature correlations for estimation of circulating temperatures for cementing.1 2
To use the current API bottomhole temperature circulation correlation schedules for design of the cement slurry thickening time, for a given depth, workers must know the averaged static temperature gradient.
The current API test schedules assume that the surface formation temperature (SFT) is a constant 80° F. SFT varies considerably in the real world, however. The author recently developed a simple method that allows use of the API temperature correlations for various SFT values.3
Alternatively to the API schedules, the author suggests the use of an empirical formula, Equation 1 developed below, for estimating downhole mud circulating temperatures.
In deep, hot wells, the densities of water and oil-based muds can vary significantly from the measured values at surface conditions. Calculations have shown that bottomhole pressures, predicted with constant surface density, are often in error by hundreds of psi.
To calculate the actual hydrostatic pressure in a well, an operator must accurately determine the drilling mud density under downhole conditions. This in turn allows better predictions of bottomhole formation differential pressure and reduces fluid losses caused by miscalculated overbalanced pressures.
Thermal expansion of drilling muds, in areas with high geothermal gradients, can lead to unintentional underbalance-a kick may occur.
In a previous work, the author suggested methods for accurately determining downhole hydrostatic pressure in areas of known geothermal gradient.4 5
Wells drilled in new areas will encounter geothermal gradients that are not known. The required temperature and pressure prediction methods must, for economic reasons, obtain the required input data from temperature logs while drilling.
This work derives the methods and presents an example that uses the input data available while drilling.
Circulating mud temperature
Assuming an operator is drilling a well in an area where the temperature gradient is unknown or cannot determine the static temperature gradient with sufficient accuracy, only empirical methods are available to estimate downhole-circulating temperatures.
The temperature surveys in many deep wells have shown that both the outlet drilling fluid temperature and the bottomhole temperature vary monotonically with vertical depth.
Reference 6 suggested that stabilized circulating fluid temperature (Tm), at any point in the annulus, could be expressed as Equation 1 (see accompanying box), where C0, C1, and C2 are empirical coefficients, h is the current depth, and H is the total vertical depth.
The C0, C1, and C2 values depend on the details of the drilling operations, such as the mud properties and flow rate, well design, and the drilling rate of penetration. These coefficients also depend on the geothermal gradient and thermal properties of the formations.
The equation also assumes that these parameters vary within narrow limits for a given geographical area.
For offshore wells, Equation 1 must include the riser length, DR, as it is modified in Equation 1a. The process of determining the coefficients C0, C1, and C2 for offshore wells becomes more complicated than onshore.
For the offshore environment, and from recorded surface-mud outlet temperature values, Tout, computer models can determine the "outlet" or returning mud temperature at the point where the depth, h, is equal to the riser depth, DR.
In addition to the surface outlet mud temperature records, determination of C0, C1, and C2 requires downhole temperature survey results.
The value of Tm in Equation 1 and 1a is the stabilized downhole circulating temperature. From routinely recorded outlet mud temperature logs (Tout), workers can estimate the time required for downhole temperature stabilization to occur.
Recording the values of the outlet mud temperature with time, during periods of mud circulation without penetration, one can determine the moment in time that values of Tout remain practically constant.
The results of more than 10 deep wells have verified the validity of Equation 1. The correlation has the advantage that temperature surveys in several wellbores in the same area can yield the required empirical coefficients.7
Hydrostatic pressure
In a previous work, the author developed an empirical equation-of-state for drilling muds and brines that describes the pressure-density-temperature dependence (Equation 2).8
Equation 2 relates mud density at standard conditions of zero pressure and ambient temperature of 59° F., allowing technicians to calculate mud density at downhole conditions.
Equation 3 describes the stabilized circulating mud temperature as a linear function of the vertical depth. With this assumption, Equation 4 yields the bottomhole and outlet stabilized circulating mud temperatures.
References 4 and 5 develop the general equations and explain the procedures for determining the downhole hydrostatic pressure using the Equation 2 and 3 results.
Example
A major oil company collected extensive circulating temperature data while drilling and completing a deep Mississippi well.9
Engineers measured the stabilized bottomhole circulating temperatures while drilling at total depths (H) of 16,079 ft, 21,439 ft, and 23,669 ft. They also recorded the surface or outlet mud temperature (h=0).
Table 1 presents the actual bottomhole and surface outlet or flowline temperatures recorded during logging. Researchers obtained stabilization time values (ts) from plots of the outlet mud temperature versus time.7 9
The work revealed the correlation between stabilization time and total depth as presented in Equation 5, where time is in hours and depth is in feet.
Workers had run a multiple regression analysis by computer of the three stabilized bottomhole circulating temperature measurements and the three stabilized outlet mud temperature values to obtain coefficients for the empirical formula of Equation 1, as follows:
Equation 6, therefore, calculates downhole-circulating temperatures.
The author compared the values of bottomhole and outlet-circulating temperature that were measured and calculated by Equation 6, and as shown, the measured and predicted values were in satisfactory agreement (Table 1).
Equations 7 and 8 follow from Equation 6, presenting the bottom and outlet temperatures from the well total depth.
Equation 9 gives the mud circulating temperature gradient. Table 2 presents the downhole drilling mud temperatures for the three values of the total vertical depth that are given.
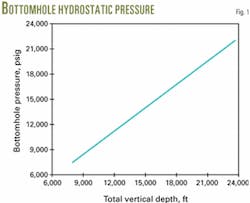
Table 3 and Fig. 1 present the results of calculations from Equations 5-9, as well as the methods explained in References 4 and 5. The well was assumed to have been drilled with water-based mud and given the following Equation 2 parameters:8 10
- ρ0 = 18.079 ppg.
- a= 3.0296 x 10-6 1/psig.
- ß= -1.3547 x 10-4 1/°F.
- γ= -4.1444 x 10-7 1/°F.2.
The author also compared values of hydrostatic pressure with the pressure assuming constant fluid density (p*) calculated by the conventional constant-surface-mud-density method, as given by Equation 10.
It follows from Table 3 that workers should take into account the effect of the temperature and pressure on drill ing mud density at downhole mud pressure predictions.
Determining the coefficients of Equation 1, therefore, allows one to forecast the downhole circulating mud temperatures and to calculate hydrostatic pressures while drilling.
References
- Covan, M., and Sabins, F., "New Correlations Improve Temperature Predictions for Cementing and Squeezing," OGJ, Aug. 21, 1995, p. 53.
- API RP 10B, Recommended Practice for Testing Well Cements, Washington, DC, 22nd Edition, December 1997.
- Kutasov, I.M. "Method Corrects API Bottomhole Circulating-Temperature Correlation," OGJ, July 15, 2002, p. 47.
- Kutasov, I.M., Applied Geothermics for Petroleum Engineers, Elsevier, 1999
- Kutasov, I.M. and Sweetman, M., 2001, "Method Predicts Equivalent Mud for HPHT Wells," OGJ, Sept. 24, 2001, p. 57.
- Kuliev, S.M., Esman, B.I., and Gabuzov, G.G., "Temperature Regime of the Drilling Wells," Nedra, Moscow, 1968
- Kutasov, I.M., Caruthers, R.M., Targhi, A.K., and Chaaban, H.M., "Prediction of Circulating and Shut-in Temperatures," Geothermics, 17, No. 4, 1988, p. 607.
- Kutasov, I.M, "Empirical Correlation Determines Downhole Mud Density," OGJ, Dec. 12, 1988, p. 61.
- Wooley, G.R., Giussani, A.P., Galate, J.W., and Wederlich, H.F., III, "Cementing Temperatures for Deep-Well Production Liners," SPE paper 13046, presented at the SPE Annual Technical Conference and Exhibition, Houston, Sept. 16-19, 1984.
- McMordie, W.C., Jr., Bland, R.G., and Hauser, J.M., "Effect of Temperature and Pressure on the Density of Drilling Fluids," SPE Paper 11114, presented to the SPE Annual Technical Conference and Exhibition, New Orleans, Sept. 26-29, 1982.
The author
I. Kutasov is a senior research engineer for Pajarito Enterprises, Los Alamos, NM. Prior to his current position, he was a senior lecturer in the school of petroleum engineering at University of New South Wales, Sydney, and a graduate faculty member in the department of petroleum engineering and geosciences at Louisiana Tech University, Ruston. He also worked for Shell Development Co., Houston, as a senior research physicist. Kutasov holds an MS in physics from the Yakutsk State University and a PhD in physics from O. Schmidt Earth Physics Institute in Moscow. He is a member of SPE.