New equation of state is accurate for VLE, PVT calculations of oil mixtures
A new cubic molecular-based equation of state (MMM) accurately calculates pressure, volume, temperature (PVT) and vapor-liquid equilibrium (VLE) data for pure and mixed fluids.
Comparisons to the Redlich-Kwong (RK) equation of state, which is considered the best two-constant-parameter equation of state, indicated that the MMM equation of state was more accurate.
This article reports application of the MMM equation of state to pure and mixed fluid calculations of interest to the oil and gas industries. Comparison of the results to those obtained using the RK and Peng-Robinson (PR) equations of state showed that MMM is more accurate.
Equations of state
Volumetric and equilibrium calculations for oil mixtures are important in separation-equipment designs. A simple, accurate equation that calculates PVT properties of oil and gas mixtures is therefore useful for design and operation purposes.
Simple theoretical equations of state to predict fluid properties are becoming more important for industrial operators. The equations of state developed must be simple and accurate enough to replace existing empirical equations of state.
Current theoretical equations of state are based on successful theories of statistical thermodynamics.1-4 Simple cubic equations of state, however, are still used for chemical engineering calculations especially in the oil and gas industries.5
We developed a molecular-based equation called the MMM equation of state.6 Comparisons showed the advantages of MMM vs. the RK equation as the best cubic, two-constant equation for pure and mixed fluid calculations.5 6
In this article, we used the MMM equation of state to calculate the density and equilibrium states for pure, binary, ternary, and oil mixture fluids. We compared results of the volumetric calculations at different temperatures and pressures with derived results from the RK equation of state.7
These comparisons showed that the MMM equation of state was more accurate than the RK equation.
The Soave-Redlich-Kwong (SRK)8 and RK equations of state give similar results for volumetric calculations; therefore we compared MMM equation of state with RK and PR9 only for calculating VLE and PVT for oil mixtures.
MMM equation of state
Equations 1-4 (see Equation box) show the MMM equation of state.5 6
This equation was previously used for PVT and VLE calculations of pure and mixed fluids. In this article, we used the MMM equation to calculate the pure and mixture densities of heavy hydrocarbons, especially at high pressures.
Equations 5-7 show simple conventional mixing rules. We used a new mixing rule for the repulsive parameter, b, based on hard-sphere theoretical considerations (Equation 8).5
If a = 1, Equation 8 reduces to Equation 7; therefore the popular mixing rule for b is a special form of Equation 8, the proposed mixing rule.
Calculations
Because PVT fluid properties play such an important role in the various steps of design and process operations, we used the MMM equation of state to calculate density calculations of pure components.
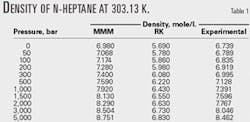
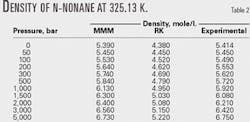
Tables 1 and 2 compare the results with the RK equation of state. These tables show that the MMM equation is much more accurate than the RK equation.
We also used the MMM and RK equations of state to calculate densities of binary and ternary mixtures. The calculation results in Table 3 show that MMM is more accurate than RK for density calculations of the evaluated systems.
We then applied the MMM equation to PVT and VLE calculations for oil mixtures and compared the results to data obtained using the RK and PR equations of state.
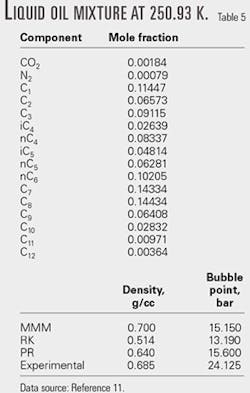
Tables 4 and 5 show the calculated results for selected oil mixtures. For all the calculations, kij equal zero.
According to our comparisons, MMM performs better than RK and PR equations for density calculations. For phase equilibrium calculations, the MMM equation of state was comparable to the PR equation; however, the MMM equation does not require accentric factor data.
For a ternary mixture (C1-C3-C10), we compared bubble point pressure calculations using MMM and RK equations of state. Table 6 shows that MMM is the more accurate of the two equations of state.
The MMM equation of state is more suitable for extrapolation purposes due to its theoretical basis.
References
- Week, J.D., Candler, D., and Anderson, H.D., "Role of repulsive forces in determining the equilibrium structure of simple liquids," J. Chem. Phys., Vol. 54, 1971, p. 5237.
- Mansoori, G.A., and Canfield, F.B., "Variational approach to the equilibrium thermodynamic properties of simple liquids," J. Chem. Phys., Vol. 51, 1969, p. 4958.
- Song, Y., and Mason, E.A., "Statistical-mechanical basis for accurate analytical equation of state for fluids," Fluid Phase Equil., Vol. 75, 1992.
- Ihm, G., Song, Y., and Mason, E.A., "A new strong principle of corresponding states for nonpolar fluids," J. Chem. Phys., Vol. 94, 1991, p. 3839.
- Mohsen-Nia, M., Modarress, H., and Mansoori, G.A., J. of Petroleum Science and Engineering, Vol. 12, 1994, pp. 127-36.
- Mohsen-Nia, M., Doctoral thesis on modification of equation of state, Amir Kabir University of Technology, Tehran, Iran, 1993.
- Redlich, O., and Kwong, J.N.S., "On the thermodynamics of solutions," Chem. Review, Vol. 44, 1949, pp. 233-44.
- Soave, G., "Equilibrium constants from a modified Redlich-Kwong equation of state," Chem. Eng. Science, Vol. 27, 1972, pp. 1197-1203.
- Peng, D.Y., and Robinson, D.B., "A new two-constant equation of state," Ind. Eng. Chem. Fundamentals, Vol. 15, 1976, pp. 59-64.
- Simenat, R., et al., "Phase behavior properties of CO2-reservoir oil system," SPE Journal, Vol. 18, No. 1, 1978.
- Bergman, David F., et al., "Retrograde condensation in natural gas pipelines," Arlington, Va.: American Gas Association, 1975.
The authors
Mohsen Mohsen-Nia is an assistant professor at Kashan University, Kashan, Iran. He has also taught and conducted research at Amir-Kabir University of Technology, Tehran. His interests are chemical thermodynamics, phase behavior, and experimental and theoretical studies on the thermodynamic properties of pure fluids and fluid mixtures. Mohsen-Nia holds an MSc (1985) and PhD (1993) from Amir-Kabir University of Technology.
Hamid Modarress is an assistant professor at Amir-Kabir University of Technology, Tehran, where he has worked for the past 28 years. His interests are chemical thermodynamics and statistical mechanics with an emphasis on phase equilibrium of fluid mixtures. Modarress holds an MSc (1972) and PhD (1975) from University College of Swansea, UK.
G.A. Mansoori is a professor of chemical engineering at the University of Illinois, Chicago. He was a postdoctoral fellow at Rice University, Houston, from 1969-70. He holds a BS from the University of Tehran, an MS from the University of Minnesota, and a PhD from the University of Oklahoma, all in chemical engineering.