Pipeline Design Tools - 1
A new equation for accurate approximation of the Moody friction factor in the general gas-flow equation better approximates a wide range of Reynolds numbers than previously published equations. Other, less-accurate explicit approximations to the Moody friction factor have been widely used because they allow the gas-flow equation to be solved directly instead of iteratively.
For actual computation of the best values of design variables, it is necessary to express a gas-flow equation and consequently a friction-factor equation that are valid for all practical operating conditions.
The older empirical gas-flow equations have used various coefficients and exponents for friction-factor estimation. These equations represent the flow conditions upon which they were derived but may not be accurate under different conditions.
Because most of actual gas pipelines operate in turbulent flow regime (at high Reynolds numbers usually between 5 X 104 and 5 X 107), the value of each previous friction factor will be higher than its actual amount. (The sloped line portion is higher than the horizontal portion of the Moody diagram.) And, the actual pressure drop will be higher than calculated.
But, the new equation presented here, which has been adjusted for the flow in actual pipelines, is valid for Reynolds numbers between 5 X 104 and 5 X 107 allowing more accurate design of gas transmission pipelines.
This article is the first of two that present new and simpler pipeline design approaches. The conclusion next week discusses a simpler correlation for predicting liquid holdup in gas condensate, two-phase flow pipelines.
Analysis
Optimum design of gas transmission pipelines requires an accurate method for predicting pressure drop for a given flow rate or predicting flow rate for a specified pressure drop (OGJ, Mar. 8, 1995, p. 70). The relationship between the gas flow rate and pressure drop in gas transmission pipelines is given by the well known Moody equation (Equation 1 in the accompanying box).1 2
Determining this equation assumes that there is no elevation in the pipeline and the condition of flow is steady-state and isothermal. All of these assumptions are usually satisfactory on the typical long pipeline.
This equation, however, usually contains an efficiency factor, E, to correct for these inaccuracies.3 Most experts recommend using values of 0.9 to 0.92 for E when dry gas flows through new pipeline. As the pipe ages and becomes subject to various degrees of corrosion, the efficiency will decline, even for dry gas.4
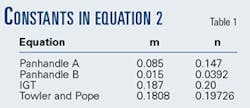
In Equation 1, the Moody friction factor, f, which is well established in graphical form or in mathematical form, must be determined from a simplified explicit equation. The most widely published friction-factor approximations are the Weymouth, Panhandle A, Panhandle B, IGT,5 6 and Towler and Pope equations (OGJ, Apr. 4, 1994, p. 55).
Because the Weymouth equation is a straight line on the Moody diagram, its approximation has been shown to be a poor estimator of friction factor for most flow conditions and should not be used. The remaining four equations approximate the Moody friction factor by Equation 27 in which constants m and n are given in Table 1.
In these approximations, the Reynolds number, NRe, is calculated by Equation 3.
The previously mentioned studies indicate a significant ordering of friction-factor data with the Reynolds number. In this study, this ordering was used as the basis for developing the friction factor based on the Moody smooth-pipe friction factor data for Reynolds numbers between 5 3 104 and 5 3 107, which covers practically all the gas transmission pipelines, and yielded Equation 4.
Combining this friction-factor approximation with Equation 1 yields the specific gas-flow equation shown in Equation 5.
The constants (a1 to a5) depend on the approximation used for the friction factor; Table 2 gives their values for Equation 5.
As Table 2 shows, the gas flow rate does not depend on the viscosity at high Reynolds numbers. Thus, once the gas viscosity is determined for an operating pipeline, small variations from the conditions under which it was determined will not influence the accuracy of the equation's applicability.
In other words, under normal conditions, the viscosity term will not greatly influence the results because a 30% change in absolute value of the viscosity will cause only about 2.7% change in the computed quantity of gas flowing.7
Results
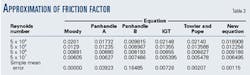
The friction-factor approximations were evaluated by comparing them with the Moody friction factor for smooth-pipe flow (Table 3). The Reynolds number varied from 5 X 104 to 5 X 107.
An equation8 was used to generate the Moody smooth-pipe friction factor. This equation has an average deviation factor of 0.0002% and a maximum deviation of 0.0023%.
Notice that in this study, the range of applicability for the friction-factor approximations will be defined as a simple mean error of ±0.0012 from the Moody smooth-pipe friction factor. The simple mean error is a measure of the overall centering or accuracy of the predicted values with respect to the base values because positive and negative errors have a canceling effect.
Therefore, as shown in Table 3 for the investigated Reynolds numbers, the new equation was superior for predicting the Moody friction factor.
References
- Moody, L.F., "Friction Factors for Pipe Flow," ASME, 1944.
- Schroeder, D.W., "A Tutorial on Pipe Flow Equations," Stoner Associates Inc., Carlisle, Pa., Aug. 16, 2001.
- Campbell, J.M., Gas Conditioning and Processing, 3rd Edition, Campbell Petroleum Series, Norman, Okla.: University of Oklahoma Press, 1972.
- Brill, J.P. and Beggs, H.D., Two-Phase Flow in Pipes," 6th Edition, Tulsa, Okla.: Tulsa University Press, 1991.
- Kennedy, J.L., Oil and Gas Pipeline Fundamentals, Tulsa, Okla.: PennWell Publishing Co. 1984, pp. 76-79.
- Beggs, H.D., "Gas Production Operations," OGCI, Tulsa, pp. 100-10 (1984).
- Huntington, R.L., Natural Gas and Natural Gasoline, New York: McGraw-Hill Book Co., 1950.
- Serghides, C.K., "Estimate Friction Factors Accurately," Chemical Engineering Journal, Mar. 5, 1984.