Correlations developed for compressibility
Two separate correlations for predicting the isothermal compressibility of reservoir fluids and crude oils have been developed. One correlation is based on molecular weight; the other, on API gravity.
Isothermal compressibility and its reciprocal, the bulk modulus, of liquids are physical properties important in the design of process equipment handling liquids at high pressure.
Their determination has specific applications in the transfer of crude oil containing dissolved gas components from a reservoir to a gas-oil separation plant and the pipeline transportation of degassed liquids such as crude oils and refined products. Experimental data for the isothermal compressibility of such mixtures are seldom readily available.
The two correlations that have been derived are of equal accuracy and require only the molecular weight or API gravity of the liquid and its density at standard conditions. They provide predictive methods to calculate the isothermal compressibility of a liquid mixture and, from it, the compressed liquid volume.
The absolute average deviations in the calculated isothermal compressibility and compressed liquid volume are 15% and 0.4%, respectively
Applications
For most practical purposes, the assumption that liquids are "incompressible" is quite acceptable. All liquids, however, undergo some reduction in volume when subjected to sufficiently high pressures. The isothermal compressibility of liquids decreases with increasing pressure. At constant pressure, the compressibility increases with temperature and increases rapidly as the critical temperature of the liquid is approached.
Two specific areas of interest in oil and gas operations in which knowledge of isothermal compressibility or its reciprocal, the bulk modulus, of a liquid is important are the transfer of produced fluids (oil with its dissolved gas components in a pipeline from a reservoir to the gas-oil separation plant) and pipeline transportation of liquids such as crude oils and refined products.
Crude oil, with its dissolved gas components, is generally present in reservoirs at very high pressures, often several thousand pounds per square inch greater than the fluid mixture's bubble pressure. The bubble pressure is the pressure above which the mixture is a single liquid phase.
When this fluid mixture is produced and allowed to flow to surface gathering facilities, it undergoes a reduction in pressure and simultaneously expands in volume, even while still in the liquid phase.
The expansion factor, which is the ratio of the volumes of unit mass of the fluid at the higher and lower pressures, can have a direct bearing on the required dimensions of the processing equipment and associated piping.
Crude oil and refined products such as diesel and gasoline are commonly pumped through pipelines for transportation from one point to another.
An important consideration in the design of pipelines for liquids transportation is protection of the pipeline from pressure surges that can be generated by pump trips or inadvertent closures of valves during normal operation. The magnitude of the pressure surge is proportional to the bulk modulus of the liquid.
Protection is usually provided either by an adequate pipe wall thickness or by appropriate surge-relief equipment. The magnitude of the liquid bulk modulus is therefore important in pipeline design.
Accurate knowledge of the liquid isothermal compressibility is seen to be important for design of equipment in the cases discussed previously. Experimental liquid isothermal compressibility data for these mixtures are not widely available.
In current engineering practice, equipment designs are accomplished with process-simulation programs in which the fluid properties are represented by equations of state.
The Soave-Redlich-Kwong and Peng-Robinson equations of state are two of the more widely used. These equations are known to be of limited accuracy in calculating liquid density1 and are not accurate for liquid isothermal compressibility.
Other calculation methods, such as the API and Lee Kesler methods, based on the corresponding-states principle, or experimental measurements should then be used for accurate determination of compressed liquid density and isothermal compressibility. In the absence of experimental measurements, predictive methods of proven accuracy can provide adequate data for equipment design. Where experimental measurements are available, the predictive methods can be used to extend the applicable range of the available data.
The two predictive methods to calculate liquid isothermal compressibility described below are based on a generalized correlation derived for isothermal compressibility of pure liquids and later extended to mixtures.
Equations
Equations 1 and 2 (accompanying equations box) define the isothermal compressibility (K) and its reciprocal, the bulk modulus (B), in terms of volume (V) and pressure (P).
The pressure and volume changes are at constant temperature.
Isothermal compressibility has units of reciprocal pressure, and bulk modulus has units of pressure. Equations 3 and 4 are equivalent definitions in terms of the liquid density (r) and pressure (P).
Equation 5 is a generalized correlation for liquid isothermal compressibility, based on experimental data for several pure liquids at different temperatures.2 It relates isothermal compressibility to a characteristic density (rch) or characteristic volume (Vch). For nonpolar substances such as n-hexane, benzene, and cyclohexane, Vch is approximated by the critical volume.
For polar compounds, Vch fitted from experimental isothermal compressibility data is generally less than the critical volume. Characteristic volumes for several nonpolar and polar fluids are tabulated.2
In a further development,3 the method of Equations 5-8 was extended to the calculation of the isothermal compressibility of liquid mixtures. A characteristic volume of the mixture for use in Equation 8 was determined from a mole-fraction average of the characteristic volumes of the mixture components.
Isothermal compressibilities
The primary focus in previous work was on mixtures of two to three components of known compositions.2 3 For these mixtures, the calculation of a characteristic density was straightforward.
Reservoir fluids, crude oils, and refined products, however, are mixtures of many different constituents and their compositions are not always completely defined. Characteristic densities for these mixtures, for use in Equation 8, cannot be as readily estimated as for well-defined mixtures.
The aim in the present work is to apply the compressibility equations to reservoir fluids and crude oils and to relate the characteristic density to mixture properties such as molecular weight and API gravity, which are generally available.
Table 1 gives experimental data for reservoir fluid RF A3 at two temperatures. The isothermal compression data, compressed volume vs. pressure, show the reduction in specific volume (cu ft/lb) of the fluid as it is compressed.
For each set of isothermal data, the pressure range of interest is from the bubble-point pressure at that temperature to the highest pressure of the experimental data. For each pressure increment beginning at the bubble-point pressure, the experimental isothermal compressibility can be determined from the compressed volume data, as shown in Equations 9-11.
The bubble pressure of the fluid mixture RF A3 at 100° F. is 1,500 psig (Table 1). Below this pressure, the fluid exists as a mixture of two phases, vapor and liquid, in equilibrium.
(The bubble pressure of RF A3 is relatively high because it consists of approximately 30 mole % of light gases such as methane, ethane, and propane. By contrast, the bubble pressures at 100° F. of the stripped kerosine and gas-oil streams from a typical crude oil distillation unit are around 135 psig and 120 psig, respectively.)
Isothermal compression or expansion of the fluid mixture RF A3 at pressures less than 1,500 psig results in condensation of vapor or evaporation of liquid. Hence, volume changes of the total mixture cannot be described by liquid compressibility alone at less than 1,500 psig. The isothermal compressibilities to be discussed hereinafter apply to the liquid phase alone.
Isothermal compressibilities for 10 reservoir fluids and 4 crude oils were determined from experimental data with Equations 9-11. Compression data for the reservoir fluids were of the same form as those shown in Table 1.
In addition, a complete composition analysis was available for each reservoir fluid, allowing the molecular weight to be calculated directly from the composition. For the crude oils, the compression data were also of the same form as in Table 1.
The composition data were given in terms of a boiling-point curve and an average specific gravity, which is generally the case for such liquids. The molecular weight of each crude oil was determined with standard correlations from its boiling-point curve and average specific gravity.4
Equation 5 can be rewritten as Equation 12 to find the characteristic density (rch) from the experimental isothermal compressibility and density at the bubble pressure.
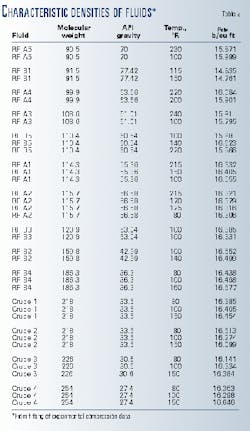
Table 2 lists the characteristic densities for the 10 reservoir fluids and 4 crude oils determined from the experimental data. The molecular weights of the liquids range from 90 to 254 and the gravities from 27° to 77° API. The characteristic densities are between 14.76 lb/cu ft and 16.65 lb/ cu ft.
The characteristic densities, molecular weights, and API gravities for 7 of the 10 reservoir fluids and 2 of the 4 crude oils in Table 2 were used in regression analyses to develop equations relating characteristic density to molecular weight and API gravity.
The regressed Equations 13 and 14 relate the characteristic density of a liquid mixture to its molecular weight and API gravity, respectively, thus making the compressibility correlation, Equation 5, completely predictive.
The density of a compressed liquid can be calculated directly from its molecular weight, or API gravity, and its density at the saturated liquid condition.
Testing the method
Isothermal compressibilities and compressed liquid volumes calculated with Equations 5, 13, and 14 for mixtures not included in the regression were compared with experimental data. Table 3 shows experimental and calculated isothermal compressibility, bulk modulus, and compressed liquid volumes for reservoir fluid RF A3 at two temperatures.
The characteristic density, 16.050 lb/cu ft, was calculated from Equation 13. The first row of each set of results in Table 3 represents the saturated liquid (bubble point) condition.
The following rows represent higher pressure conditions. At each pressure the isothermal compressibility was calculated from Equation 5. The volume and the calculated isothermal compressibility were then used in Equation 9 to calculate the volume at the next pressure.
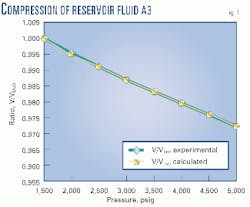
The term V/Vbub at each pressure is the ratio of the compressed liquid volume (V) to the volume at the bubble point (Vbub). There is very good agreement between the calculated and experimental values of V/Vbub. At 240° F. the calculated volume at 5,000 psig differs by only 0.16% from the experimental value.
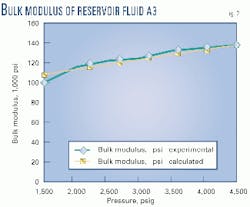
Fig. 1 is a plot of V/Vbub as a function of pressure at 100° F. There is very good agreement between experimental and calculated results. Fig. 2 is a plot of bulk modulus as a function of pressure at 100° F. Again, there is good agreement between the calculated result and experimental data.
Table 4 is a summary of the deviations between calculated and experimental bulk modulus and compressed liquid volumes for the complete set of 4 crude oils and 10 reservoir fluids listed in Table 2.
The results are separated into two sets.
The first set consists of the seven reservoir fluids and two crude oils whose characteristic densities were used in the regression analyses to derive Equations 13 and 14.
The second set consists of the three reservoir fluids and two crude oils not included in the regression analyses. The overall absolute average deviations in the two sets of results are almost equal. This agreement between the deviations for the two sets of results validates the use of Equations 5, 13, and 14.
The overall absolute deviations with the molecular-weight correlation (Equation 13) and the API gravity correlation (Equation 14) are almost equal, for both sets of fluids. Therefore, the two equations may be considered to be of equal accuracy in predicting the isothermal compressibility and compressed liquid volume.
Pressure-surge analysis
As mentioned, an important application of liquid compressibility or, alternately, bulk modulus is in calculating pressure surges in pipelines under inadvertent closures of pipeline valves.
Commercially available software packages for pipeline simulation provide the means to calculate pipeline pressures at steady-state and dynamic conditions. The input data required are the flowing fluid's properties and flow rate and the mechanical details of the pipeline system.
Simulations were carried out for two different pipeline systems transporting crude oils. For each system, the simulation was first performed with a liquid bulk modulus calculated from Equations 5 and 14 and then repeated with a laboratory-measured bulk modulus.
The first system is relatively simple consisting of a storage tank feeding two parallel shipping pumps. The pumps discharge into a common header from which the flow is divided into two approximately 30,000-ft pipelines, one 6 in. and the other 8 in. OD.
The pipelines combine at the downstream end to feed a receiving storage tank through a tank inlet valve. The simulation determines the peak pressure buildup in the pipeline when the tank inlet valve is inadvertently closed.
The second system is somewhat more complex.
Crude oil storage tanks at the source feed two shipping pumps each discharging into separate pipelines. The two pipelines run parallel to each other for approximately 50 km at which point they are connected by a "jumpover," which also feeds a third pipeline.
About 70 km further downstream are more interconnections between the three pipelines. At a point 30 km still further downstream, the three pipelines discharge through a common distribution header into the receiving storage tank through a tank inlet valve.
The dynamic simulation then determines the peak pressure buildup in the pipeline when the tank inlet valve is inadvertently closed.
Table 5 shows simulation results. The maximum pressure increase calculated using a bulk modulus from Equations 5 and 14 agrees very closely with that calculated with a laboratory-measured bulk modulus.
This agreement demonstrates that Equations 5 and 14 may be used to generate a bulk modulus for pipeline simulations in the absence of experimental data.
Accuracies
The generalized compressibility correlation (Equation 5) can be combined with the relation between characteristic density and molecular weight (Equation 13) or the relation between characteristic density and API gravity (Equation 14) to give a completely predictive method to calculate the liquid isothermal compressibility and the compressed liquid volume.
A solution is generated by supplying values for the volume of the saturated liquid at the same temperature and its molecular weight or API gravity. The calculated compressed liquid volumes will be within 0.5% and the calculated isothermal compressibilities within 15% of the experimental values.
Equations 13 and 14, relating characteristic density to molecular weight and API gravity, respectively, are equally accurate in predicting the isothermal compressibility and compressed liquid volume.
In the absence of experimental data, the methods provided here are useful in estimating isothermal compressibility, bulk modulus, and compressed liquid volumes of reservoir fluids and crude oils for equipment design.
Acknowledgments
The author gratefully acknowledges Saudi Aramco for its approval to publish this article, Jack Dempsey for reviewing the first draft of the manuscript, and Hadeel Al-Rabeh for running the pipeline simulation cases.
References
- Reid, R.C., Prausnitz, J.M., and Poling, B.E., The Properties of Gases & Liquids, 4th Edition, New York, McGraw Hill, 1987.
- Brelvi, S.W., and O'Connell, J.P., "Corresponding States Correlations for Liquid Compressibility and Partial Molar Volumes of Gases at Infinite Dilution in Liquids," AIChE Journal, Vol. 18, 1972.
- Brelvi, S.W., and O'Connell, J.P., "Prediction of the Isothermal Compressibility of Liquid Mixtures," AIChE Journal, Vol. 21, 1975.
- API Technical Data Book, 1980.
The author
S. Waseem Brelvi is recently retired from Saudi Arabian Oil Co., Dhahran, for which he was most recently an engineering specialist with the pipelines and flare systems unit, process engineering division. Brelvi holds a PhD in chemical engineering from the University of Florida and is a member of AIChE.