FRACTURE PROPAGATION— Conclusion: Prediction steel grade dependent
Battelle’s two-curve method (TCM) fracture arrest predictions for X70 grade steels and higher requires a correction factor for the predictions to be accurate and useful for selecting pipe steels. The first part of this article (OGJ, Oct. 20, 2008, p. 52) examined three correction factors: Leis, Wilkowski, and Centro Sviluppo Materiali (CSM). This concluding article will show the appropriate factor to be grade-specific.
Background
Fracture initiation occurs when a flaw exists in a pressurized pipe that is the maximum size flaw for the toughness level of the pipe at the operating stress level in the pipe. A deep enough and short enough flaw will result in a stable leak when it penetrates the pipe’s WT. A sufficiently long and shallow flaw penetrating enough of the WT will begin to propagate along the length of the pipe.
If the pipe is operating at less than its transition temperature (i.e., 85% shear area transition temperature, SATT) in the drop-weight tear test (DWTT), the fracture will be brittle and will propagate at high speeds and possibly over long distances (miles). If the pipe is operating at greater than DWTT 85% SATT, it will be ductile and the propagation or arrest will depend on its toughness (Charpy V-Notch impact energy, CVN).
TCM contrasts the fracture speed and pressure curves for a pipe with a given toughness against the gas decompression speed curve and pressure providing the driving force for the fracture.
Testing
Testing the X70 steels showed the Leis factor to be the least conservative and CSM the most conservative for the steels examined, with the Leis factor emerging as a reasonable correction factor to apply. A factor between Leis and Wilkowski appears to be necessary for X80 control-rolled steels, and a modification of the Leis factor is proposed later in this article. The modification increases the conservatism of the Leis equation but leaves it lower than the Wilkowski factor.
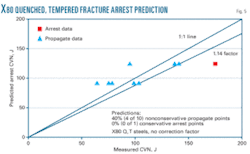
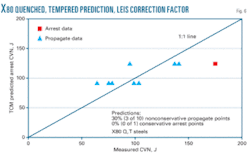
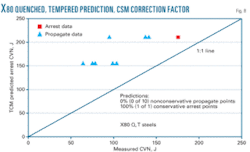
Insufficient data exist to define what factor is needed for X80 quenched and tempered steels.
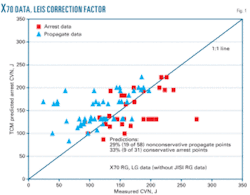
Figs. 1 and 2 show X70 lean and rich gas test data, including the TCM predictions corrected by Equations 1 and 2, respectively. Fig. 1 shows the Leis correction factor resulted in nonconservative propagate and conservative arrest data points with about the same percentages, creating a usable average correction factor.
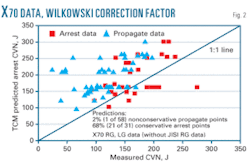
Fig. 2 shows the Wilkowski correction factor applied to lean and rich gas X70 data, demonstrating that the Wilkowski correction factor is more conservative than the Leis factor, with only 2% of nonconservative propagate data lying outside the correction. The increase in the conservative arrest point to 68% demonstrates this more conservative status, offering users a more conservative choice than the 1.7 factor proposed by CSM.
Fig. 3 shows the CSM correction factor applied to the lean and rich gas X70 data, demonstrating it to be the most conservative of the three, with 5% nonconservative propagate data and 0% conservative arrest data. These results seem extremely conservative, so much so that the required pipe toughness may be unavailable from mills.
Fig. 4 compares the correction factors for CSM, Leis, and Wilkowski. The CSM correction starts as the highest until a TCM CVN of 170 J is reached, at which point the Wilkowski correction becomes the highest. The Leis correction is the lowest of the three.
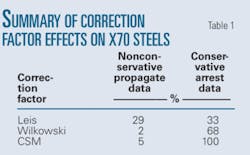
Table 1 summarizes the results of the correction factor effects on the X70 steels for lean and rich gases. The table shows that as the conservativeness of the correction factor increases, the percentage of conservative arrest data increases. The Leis factor appears to be about right for the X70 control-rolled steels examined, based on the observation that it lies between the nonconservative and conservative data.
null
null
null
null
X80 predictions
The balance of this article will discuss the factors that control fracture arrest for X80 pipe and address application of the existing formulations to predicting the arrest toughness of X80 pipe. Available X80 burst test data all involve lean gas. Applying the following information to rich gas must therefore be done with caution, as data from X70-grade pipes showed the possibility that predicted arrest toughness may have to be higher for rich gas than had been determined for lean gas. The predictions are also only valid for steels exhibiting a relatively flat upper shelf in the CVN curve.
All of the X80 data presented applies to control rolled or thermomechanically processed steels as did all of the X70 steel data presented previously. Table 2 shows the X80 tests performed. Table 3 summarizes the effect of the correction factors on the X80 steels.
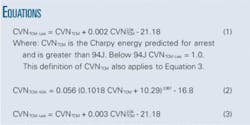
Table 3 offers two observations. The various factors have a different effect on the higher-grade pipe, suggesting that a factor should be grade specific. The Leis factor also does not have any conservative arrest data, while the Wilkowski and CSM factors appear too conservative with only 7% nonconservative propagate data points. Equation 3 shows a proposed revision to the Leis correction factor for X80 controlled rolled steels, increasing the multiplier from 0.002 to 0.003.
It would be nice to have zero nonconservative and conservative data points, but the present status of predictive capabilities coupled with the variability in toughness properties leads to scatter in the full-scale test results that cannot be eliminated. This suggests that a correction factor averaging the nonconservative propagate data and the conservative arrest data is about as good as can be expected.
Not every length in a pipeline has to arrest a fracture for fracture control to be achieved. Specifying the predicted TCM arrest level as a minimum value for a pipe order will ensure all pipe has a toughness level that exceeds the minimum specified value.
Quenched, tempered
The final assessment is based on X80 quenched and tempered steels. Having only 11 data points minimized the scatter. Figs. 5-8 show a comparison of the measured CVN energies of the pipes in full-scale tests vs. the TCM predicted CVN arrest energies. With the few data points available, even the uncorrected data are in reasonable agreement. But the X80 control-rolled-steel results demonstrate the need for a correction factor.