New method predicts bottom-water breakthrough time
Haitao Li
Yahui Li
Ying Li
Southwest Petroleum University
Chengdu, China
Jibin Zhong
Changquing Oil Field Co.
Xi'an, China
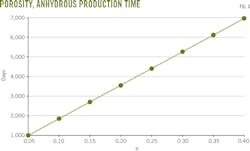
Anhydrous production time increases with growing reservoir porosity. The relationship between porosity and the anhydrous time is linear. Coning reduces oil production as water enters the perforation zone in the near-wellbore area. Pressure forces fluids toward the wellbore, overcoming the natural separation of the oil-water contact (OWC).
Extensive research exists regarding how output is affected, the law of bottom-water breakthrough, the coning mechanism, and other aspects of bottom-water reservoirs.1-6
Less attention has been given to the time it takes for bottom water to break through in reservoirs with a barrier. The studies that do exist assume that the water-coning profile under the barrier is shaped like an isosceles trapezoid.7 8
This article challenges that assumption. It looks at the rising OWC as having a curved conical shape to develop a new predictive model. The article combines the pressure-drop superposition principle, Darcy's law, and seepage models of plane and spherical-radial flow, to accurately predetermine breakthrough time in a bottom-water reservoir with a barrier.
Mathematical analysis
The following five parameters describe a well that can benefit from the new model:
• The reservoir is homogeneous and anisotropic.
• The oil-water transition zone's affect has not been studied.
• Influence of gravity and capillary forces has been ignored.5
• Flow obeys Darcy's law.
• The barrier is at bottomhole.
Based on the distribution of pressure drop at bottomhole and the superposition principle of pressure drop, the oil well divides into two virtual wells (A and B) at the barrier's edge (Fig.1).10
Under pressure at the edge, the bottom water rises from its original position to the bottom of the virtual wells. The seepage model of plane radial flow,can determine the time needed for water to flow from the barrier edge. The combined time of these two stages is the bottom-water breakthrough time.
The flow pattern above the barrier is the plane radial flow. According to the principle of seepage, when the well is producing the pressure drops at the position of Virtual Well A or B (Equation 1).
According to the pressure-drop superposition principle, pressure drop, ΔPB, can be divided into two parts: ΔP*A from Virtual Well A, and ΔP*B from Virtual Well B (Equation 2).
The seepage model under the barrier, QB-S, is a spherical radial flow for both virtual wells. Equation 3 describes the resulting pressure drop and Equation 4 calculates spherical radial flow. A combination of Equations 1 and 4 determines a new flow relationship taking into account the two virtual wells (Equation 5).
Equation 6 calculates the seepage speed of water at position z away from the original OWC. With oil recovery, the original OWC will grow.6 Equation 7 shows this increase's amplitude.
Equation 8 describes the movement height of the water at position z. Using Equation 8 in place of Equation 6 and Equation 8a in place of Equation 5 calculates movement height (Equation 9).
The time needed for bottom water to flow from the original OWC to the barrier is determined by converting Equation 9 into Equation 10 and Equation 10 into Equation 11 to find Equation 12. Solving Equation 13 using Matlab yields a new analytical expression.
The time needed for bottom-water coning from a point on the original OWC (identified as D in Fig. 1) to the barrier can be found using Equation 14. After the bottom water arrives at the edge of the barrier, plane radial-flow model (regarded as the seepage model of water flowing from barrier edge to bottomhole) combines with the material flow balance principle to find the time needed by the water flowing from the barrier's edge to bottomhole (Equation 15). Equation 16 calculates breakthrough time in a bottom-water reservoir. Equations 14-16 establish a predictive model.
Model testing
Model testing in the Ordos basin in China used the new method as well as those for which results are shown in the accompanying table.4 7
The Zhu method predicted a breakthrough time of 2,970 days with a relative error of 1.72%. The Li method predicted 2, 258 days with a relative error of -22.67%. This article's model determined a time of 2,912 days with a relative error of only -0.27%.
The difference between the Zhu method and this paper's is not great. Zhu, however, exceeded the actual time of water breakthrough in Ordos basin wells, potentially causing operators to miss opportunities for optimization and prevent bottom-water coning in these wells.
The Zhu prediction model is based on the hypothesis that the rising water under the barrier roughly forms an isosceles trapezoid. The shape is actually curved conical.
The height of a curved conical is higher than an isosceles trapezoid. The trapezoid model presupposes a uniform water rise while the conical model predicts sharp spikes in the amount of water. This discrepancy leads to trapezoid models generating prediction times longer than the actual breakthrough times. The prediction model proposed in this article is closer to the field results in the Ordos basin.
Ordos basin
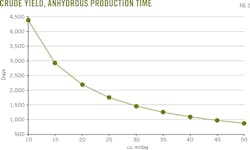
Anhydrous production time shrinks as oil yield increases. A sharp decrease in anhydrous time means bottom water will rise rapidly to bottomhole. As oil yield increases, the magnitude of the anhydrous production time decrease will stabilize gradually (Fig. 2).
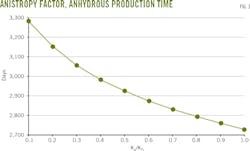
Anhydrous time-of-production also shortens with increasing reservoir anisotropy. The rate of decrease in anhydrous production time accelerated in Ordos wells with a reservoir anisotropy coefficient < 0.5, but was linear in wells with a coefficient > 0.5 (Fig. 3).Porosity rises evenly as anhydrous production time increases (Fig. 4).
Acknowledgment
The authors would like to acknowledge the support China's National Science and Technology Infrastructure Program(Grant Nos. 2016ZX05021005, 2016ZX05009003-011-002, 2016ZX05017005-003).
References
1. Sobocinski, D.P. and Cornelius, A., "Correlation for Predicting Water Coning Time," Journal of Petroleum Technology, Vol. 17, No. 5, May 1965, pp. 594-596.
2. Zhang, X.G., and Sun, W., "A study on the elimination of barrier to bottom water coning," Journal of Northwest University: Natural Science Edition, Vol. 29, No. 2, February 1999, pp. 149-152.
3. Yu, G. Ling, J., Jiang, M., Liu, D., "Production mechanism and development tactics on sandstone reservoirs with bottom water," Acta Petrolei Sinica, Vol. 18, No. 2, Apr. 25, 1997, pp. 61-65.
4. Li, C.L., "Prediction formula for water breakthrough time of partition bottom water reservoir," Petroleum Geology & Oilfield Development in Daqing, Vol. 16, No. 4, July 1997, p. 50.
5. Tang, R.X., "Simulation of Water Coning Performance and Prediction of Water Breakthrough Time in Bottom-Water Reservoir," Xinjiang Petroleum Geology, Vol. 24, No. 6, November-December 2003, pp. 572-573.
6. Wheatley, M. J., "An Approximate Theory of Oil-Water Coning," SPE Annual Technical Conference and Exhibition, Las Vegas, Sept. 22-25, 1985.
7. Zhu, S.J., "Improvement of forecasting formula for water breakthrough time in baffle based bottom-water reservoir well," Petroleum Geology & Oilfield Development in Daqing, Vol. 18, No. 3, March 1999, pp. 36-37.
8. Zhao, X.Z. and Zhu, S.J., "Prediction of water breakthrough time for oil wells in low-permeability bottom water reservoirs with barrier," Petroleum Exploration and Development, Vol. 39, No. 4, April 2012, pp. 472-473.
9. Li, X.P., "Seepage Mechanics of Underground Oil and Gas," Petroleum Industry Press, Beijing, 2008.
10. Li, C.L., "Fundamentals of Reservoir Engineering," Petroleum Industry Press, Beijing, 2005.
EQUATIONS
NOMENCLATURE
h = Reservoir thickness, m
hp = Open thickness of the reservoir, m
hb = Height away from the original oil-water contact to barrier, m
re = Radius of drainage, m
rb = Radius of barrier, m
Swi = Original irreducible water saturation
Sor = Residual oil saturation
α = Anisotropy factor, Reservoirs vertical and horizontal permeability ratio
tbt = Water breakthrough time, d
tv = Time needed by water rising from the oil water contact to barrier edge, d
th = Time needed by water flowing from the barrier edge to the bottom hole, d
Q = Oil production underground, m³/d
μ = Oil viscosity, mPa∙s
K = Reservoir permeability, D
∆PB = Pressure drop at the barrier edge position B
produced by oil well, MPa
∆P*B = Pressure drop at position B produced by virtual
well A, MPa
∆P*A = Pressure drop at position B produced by virtual
well B, MPa
PREDICTION RESULTS, ORDOS BASIN BREAKTHROUGH TIMES
Method Break through time, days Relative error, %
Li 2,258 -22.67
Zhu 2,970 1.72
Authors 2,912 -0.27
The authors
Haitao Li is a professor at the Oil and Natural Gas Engineering Institute of Southwest Petroleum University (SWPU). His research interests include horizontal wells with water-control completion, perforation completion, and sand-control completion. He holds a BS, MS, and PhD from SWPU.
Yahui Li ([email protected]) is a doctoral degree candidate at the Oil and Natural Gas Engineering Institute at SWPU. He has studied EOR theory and technology, water-control completion, and has written and published several papers related to petroleum engineering. Li holds a BS from Xihua University and an MS degree from SWPU.
Jibin Zhong, is an engineer for the Exploration and Development Institute of Petrochina Changqing Oilfield Co. He is engaged in ultra-low permeability reservoir log interpretation and comprehensive evaluation. He holds an MS in engineering from China University of Petroleum, East China..
Ying Li is a PhD candidate at SWPU. Her area of interest is enhanced oil recovery. She holds a MS in engineering from SWPU.
Shiyan Zhu is a doctoral degree candidate at SWPU's School of Petroleum and Natural Gas Engineering. She has studied water-control completion and multifracturing completion of horizontal wells. She holds an MS in petroleum engineering from SWPU.