Correlation for natural gas heat capacity developed
Mahmood Moshfeghian
John M. Campbell & Co.
Norman, Okla.
To develop a generalized correlation for natural gas heat capacity, the author conducted an extensive investigation of heat capacity as a function of temperature, pressure, and composition. To aid in understanding the impact of variables on heat capacity, the existing phase for each case was determined.
Heat capacity is widely used for heat-exchanger duty determination in plant and engineering calculations.
As expected, abnormal behavior was evident at low temperature, at which two-phase gas and liquid co-existed, and at high pressures when the system was in dense phase. These abnormalities vanished for lower relative-density natural gases, when the system was a single compressible vapor for all conditions studied. In the two-phase region of gas and liquid, the concept of a single-phase heat-capacity value does not apply; thus these values were not used to develop the correlation.
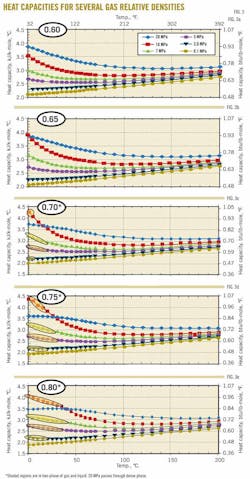
Five charts estimate the real heat capacity of natural gases with relative densities of 0.6 to 0.8 with 0.05 increments. Each chart has five isobars applicable for wide ranges of pressures (0.2-20 MPa) and temperature (0-200º C.).
In addition to these charts, two sets of correlations were developed. The first set consisted of five correlations, each unique to a specific relative density. The last correlation is general and a function of all three variables (temperature, pressure, and relative density). These charts and correlations are based on rigorous computer calculations.
The accuracy of these correlations is compared with the computer calculation results obtained by two commercial process simulators and relatively good agreements have been obtained.
Exchanger duty
To yield the heat load (Q) for a heat exchanger, heat capacity (CP) at system pressure and average temperature is multiplied by gas mass flow rate and temperature change (ΔT). It is also used to determine heat capacity ratio (k = CP/CV), which is needed for compressor power and isentropic head calculations. It can be used to estimate compressor discharge temperature. Heat capacity ratio is also used to calculate the sonic velocity of gases through nozzle and orifice.
Numerous sources present correlations for estimating ideal gas heat capacity of pure compounds. In general, the accuracy of these correlations is very good, with error in the range of 1-2%. For real gases, however, there is not much choice except to use equations of state (EOS). For these gases, heat capacity depends on temperature, pressure, and composition. The expressions of heat capacity for real gases based on an EOS are complicated and not suitable for calculation by hand.
The change in enthalpy for a fluid when no phase change occurs between Points 1 and 2 can be expressed as shown in Equation 1 of the accompanying equations box.
The second term on the right hand side of this equation is generally not convenient to solve manually. However, it is trivial or zero for the following cases:
• Ideal gases.
• Constant pressure, dP = 0.
• For a liquid considered incompressible.
For all three cases, enthalpy is a mathematical function only of temperature. Cp is commonly expressed by equations of the form of Equation 2. In most instances it is sufficiently accurate to find a CP at the average temperature TAvg (Equation 3). CPAvg is then found at this average temperature (Equation 4).
This approximate solution to the first integral, although inexact, is satisfactory for most applications. Heat capacity values for pure substances are readily available from many handbooks and similar reference material. As noted in Chapter 7 of Volume 1, Gas Conditioning and Processing,1 values of heat capacity can be found from the slope of h vs. T plots at a given pressure. The CP for hydrocarbon liquid mixtures may be estimated from Equation 8.7 in Volume 1.1
For a nonideal, compressible fluid such as natural gas, the second term on the right hand side of Equation 1 can't be ignored. Therefore, in process simulation software, an equation of state such as Soave-Redlich-Kwong (SRK)2 or Peng-Robinson (PR)3 is used to calculate h. The enthalpy departure of a fluid mixture from the ideal gas state, for instance for PR equation of state (EOS), can be written as shown in Equation 5.
The value of the enthalpy of the fluid (h) is obtained by adding this enthalpy of departure (Δh/RT in Equation 5) to the ideal gas enthalpy (ho). Ideal enthalpies (ho) are sole functions of temperature. Therefore an analytical relationship for CP can be derived by taking the derivative of Equation 5, as shown in Equation 6. The derivative terms in Equations 5 and 6 can be found elsewhere.4
For hydrocarbons, Passut and Danner developed correlations for ideal gas properties such as enthalpy, heat capacity and entropy as functions of temperature.5 Passut and Danner reported the values of B, C, D, E, and F for 89 pure compounds (mostly hydrocarbons) for their proposed correlation in the form of Equation 7. (Note: B here is not the same as in Equation 6.)
Two years later, Haung and Daubert reported these parameters for 57 additional pure compounds.6 Also, based on statistical mechanical formulas and with simplifications to facilitate engineering calculations, Aly and Lee presented equations for calculating the ideal gas heat capacity, enthalpy, and entropy.7 Their equation for Cpo is Equation 8.
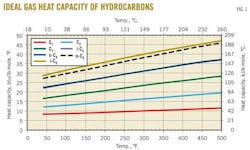
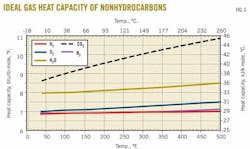
Aly and Lee reported the values of B through F for 60 pure compounds and later Fakeeha et al. reported values of these constants for 32 additional hydrocarbons.8 Based on the Aly and Lee model, the variation of the ideal gas heat capacity of several hydrocarbons (methane through pentanes) and nonhydrocarbons (O2, N2, H2, CO2, and H2O) as a function of temperature are presented in Figs. 1 and 2.
For many calculations involving the heat capacity of natural gas, Fig. 8.3 in Volume 1 is appropriate.1 Heat capacity at system pressure and average temperature is read off the graph and multiplied by gas mass flow rate and ΔT to obtain the heat load (Q); Equation 9.
However, Fig. 8.3 in Volume 1 gives approximate values of natural gases with relative densities from 0.65 to 0.75.
This article demonstrates the variation of the heat capacity of natural gases with temperature, pressure, and specified relative density (composition) and presents an empirical correlation to account for these variations.
This correlation will be used for estimating natural gas heat capacity for wide ranges of pressure, temperature, and relative density. Finally, the accuracy of the proposed correlation will be discussed.
Generalized correlation
As mentioned earlier, CP is the slope of an isobar on the h vs. T plot. Mathematically, this is expressed by Equation 10.
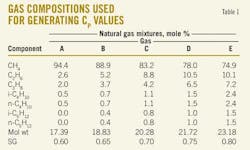
The derivative on the right hand side of Equation 10 may be obtained from an equation of state similar to Equation 6, but it is too tedious for hand calculations. Therefore, the PR EOS option in ProMax9 was used to generate CP values for various values of pressure, temperature, and relative density. The total number of CP values calculated was 715. Table 1 presents the composition of five different natural gas mixtures used in this study.
Figs. 3a-3e present variations of CP with pressure, temperature, and gas relative density. The red highlighted regions in Figs. 3c-3e identify the two-phase region of gas and liquid at which the CP concept is not valid. It should be noted that the isobar of 20 MPa represents a single phase even at low temperatures. At low temperatures, however, the fluid is in a dense phase.
In order to correlate all the curves shown in Fig. 3 by a single equation, the expression in Equation 11 is proposed.
A nonlinear regression algorithm determined the optimum values of parameters "a" through "f." The CP values of each gas in Table 1 determined "a" through "f" for that specific gas composition. Then all of the generated CP values determined a set of generalized parameters to produce the general correlation for gases with a relative density between 0.6 and 0.8.
These parameters were tuned and rounded to best represent all five gases covering a wide range of relative density from 0.60 to 0.80. For each case, Table 2 presents the parameters and the summary of statistical error analysis. Note that the CP values of the two-phase region were not used for the regression process. The general range of this correlation is 20-200° C. (68° to 392° F.) and 0.10-20 MPa (14.5-2,900 psia).
Wide ranges
A single and relatively simple correlation has been developed to estimate the heat capacity of natural gases as a function of pressure, temperature, and relative density (composition). This correlation covers wide ranges of pressure (0.10-20 MPa, 14.5-2,900 psia), temperature (20-200° C., 68-392° F.), and relative density (0.60-0.80).
A generalized set of parameters in addition to an individual set of parameters has been determined and reported in Table 2. The error analysis reported in Table 2 indicates that the accuracy of this equation is quite good and can be used for natural gas heat duty calculations.
For the generalized set of parameters, the average absolute percentage error and the maximum absolute percent deviations for the total of 715 points are 4.34 and 23.61, respectively. The applicable ranges of the proposed correlation are shown in Table 2.
It should be noted that the concept of heat capacity is valid only for the single-phase region. In the two-phase region of gas and liquid, the concept of a single-phase heat-capacity value does not apply, thus these values were not used for the development of the correlation.
Figs. 3c-3e indicate that for low temperatures where liquid forms an irregular behavior of CP is observed.
Acknowledgment
Thanks to Wes Wright for checking the accuracy of the proposed model with the results generated by the NIST REFPROP software.
References
1. Campbell, J.M., Gas Conditioning and Processing, Vol. 1, The Basic Principals, 8th Ed., Norman, Okla.: Campbell Petroleum Series, 2001.
2. Soave, G., "Equilibrium constants from a modified Redlich-Kwong equation of state," Chem. Eng. Sci., Vol. 27 (1972), pp. 1197-1203.
3. Peng, D.-Y., and Robinson, D.B., "A New Two-Constant Equation of State," Ind. Eng. Chem. Fundamentals, Vol. 15 (1976), pp. 59-64.
4. Moshfeghian, M., "Development of a New Generalized Correlation for Natural Gas Heat Capacity," 90th Annual GPA Convention, San Antonio, Apr. 3-6, 2011.
5. Passut, C.A., and Danner., R.P., "Correlation of Ideal Gas Enthalpy Heat Capacity, and Entropy," lnd. Eng. Chem., Process Des. Develop., Vol. 11 (1972), No. 543.
6. Haung, P.K., and Daubert, T.E., "Extension of Passut-Danner Correlation of Ideal Gas Enthalpy, Heat Capacity, and Entropy," Ind. Eng. Chem., Process Des. Develop., Vol. 13 (1974), No. 2.
7. Aly, F.A., and Lee, L.L., "Self-Consistent Equations for Calculating the Ideal-Gas Heat Capacity, Enthalpy and Entropy," Fluid Phase Equilibria, Vol. 6 (1981), pp. 169-79.
8. Fakeeha, A., Kache, A., Rehman, Z., Shoup, Y., and Lee, L.L., "Self-Consistent Equations for Calculating the Ideal-Gas Heat Capacity, Enthalpy and Entropy, II. Additional Results," Fluid Phase Equilibria, Vol. 11 (1983), pp. 225-32.
9. ProMax, Bryan Research & Engineering Inc., v. 2.0, Bryan, Tex., 2007.
The authorManuscripts welcomeOil & Gas Journal welcomes for publication consideration manuscripts about exploration and development, drilling, production, pipelines, LNG, and processing (refining, petrochemicals, and gas processing). These may be highly technical in nature and appeal or they may be more analytical by way of examining oil and natural gas supply, demand, and markets. OGJ accepts exclusive articles as well as manuscripts adapted from oral and poster presentations. An Author Guide is available at www.ogj.com, click "home" then "Submit an article." Or, contact the Chief Technology Editor ([email protected]; 713/963-6230; or, fax 713/963-6282), Oil & Gas Journal, 1455 West Loop South, Suite 400, Houston TX 77027 USA. |
More Oil & Gas Journal Current Issue Articles
More Oil & Gas Journal Archives Issue Articles
View Oil and Gas Articles on PennEnergy.com