New equation calculates friction factor for turbulent flow of non-Newtonian fluids
Tests of a proposed friction-factor equation have shown it to be accurate for calculating pressure loss in turbulent flow for a pipeline transporting a non-Newtonian fluid, such as most crude oils and petroleum products.
The accuracy of the proposed equation was checked statistically and by measured and field-calculated data.
Turbulent pressure loss due to friction in any pipeline can be calculated only if the friction factor is first determined. Determining this factor poses a significant problem for a pipeline engineer designing for non-Newtonian fluids because of the large number of friction-factor equations available in the literature.
The present research work set out to compare among the different friction-factor equations and propose an accurate one.
The results led to proposal of a regression equation for calculating the friction factor based on the available measured data.
Determining pressure loss
A great number of the world's pipelines transport pseudoplastic oils. Design for these pipelines requires knowing an adequate relationship for these fluids' resistance to turbulent flow. The essential problem is determining the friction factor in the Darcy-Weisbach equation that is used to determine pressure loss due to friction in any pipeline transporting fluids (Newtonian and non-Newtonian).
This equation can be written as shown in Equation 1 in the accompanying equations box. The pressure loss due to friction can be estimated if the friction factor is known.
For non-Newtonian fluids flowing in laminar flow in pipes, Metzner and Reed have suggested Equation 2 to estimate the friction factor in its Blasius form.1
For turbulent flow, however, different relationships have been developed for turbulent friction factor. Because selecting the friction-factor formula from among the many published ones is difficult, the main objective of the present research work was to search for the different friction-factor formulas, compare among them, and develop a new one.
To achieve this objective, we used available measured friction-factor data with statistical analysis2 and developed a computer program to perform the comparisons among the formulas.
The data used in this research work are divided into two groups: friction-factor measured data and pressure loss-flow rate field data.
Measured friction-factor data factors were:
- Dodge and Metzner: friction-factor values at flow behavior indices (N´) of 0.617, 0.726, and 1.0 at different values of Reynolds numbers (Re).3 4
- Shaver and Merrill: friction-factor values at flow behavior indices of 0.6, 0.8, and 0.9 at different values of Reynolds numbers.5
- Yoo: experimental friction-factor data at flow behavior indices of 0.6753, 0.7295, and 0.8382 at different values of Reynolds numbers.6 7
- Szilas: friction-factor values at flow behavior indices of 0.5287, 0.6991, 0.7169, 0.831, and 0.948 at different values of Reynolds numbers.8
The pressure loss-flow rate data used in this research work were taken from the Melieha—El-Hamrah pipeline for three samples of Egyptian crude oils.9
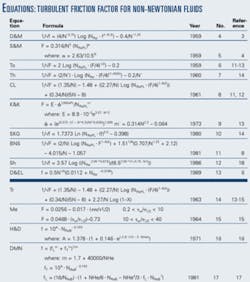
The accompanying box shows the 14 different friction-factor equations available in the literature for determining the turbulent friction factor for non-Newtonian fluids flowing in petroleum pipelines. The large number of equations may confuse any pipeline engineer when selecting the most accurate one to be used to determine the pressure loss due to friction in any pipeline.
The present research effort sought to avoid this obstacle by selecting the most accurate equation among all the published ones.
Review of the available literature indicated 10 of the 14 equations (shown above the bold line in the box) can determine the friction factor as a function of Metzner and Reed Reynolds number (NRe´) and the flow behavior index (N´). (For a Newtonian fluid, N = 1; the more N deviates from 1, the more non-Newtonian is the fluid.).
Although some of these equations are functions of the power law Reynolds number (NRepl), they can easily be written as functions of NRe´.7 8
Evaluating the equations
Input data for the computer program developed to compare among the equations used the two parameters: Reynolds number and flow behavior index. The output data were the values of the friction factor at different values of Reynolds number and also at different values of flow behavior index. These values were calculated from the different 10 equations.
Evaluation of the different published equations would be in three steps based on the available measured data.
The first step involved a visual comparison achieved by the computer program's calculation of the friction-factor values by the different equations and illustrated on the same figures with the measured values.
The second and the third steps used statistical analysis (percent mean deviation, PMD; percent standard deviation, PSD; and Error %) for evaluating the different equations.
The computer program calculated the values of the friction factor at the same conditions as the measured values and plotted on the same figures.
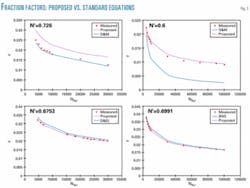
The friction factors measured by Dodge and Metzner at different values of NRe´ and N´ were taken as the basis of comparison. As an example, Fig. 1a shows the comparison between the values calculated by the 10 equations along with those measured at N´ = 0.726.
As Fig. 1a shows, the most accurate is the D&M equation, followed by D&EL, and Shenoy equations, respectively. The Clapp equation gives reasonable, but higher, values of the friction factor.
The S&M equation gives the smallest values of friction factor, followed by BNS and Thomas equations, while Tomita gives the highest ones, followed by SKG.
The K&K equation gives higher values as the Reynolds number increases and smaller values as it decreases.
- The friction factors measured by Shaver and Merrill at different values of NRe´ and N´ were taken as the basis of comparison. For example, Fig. 1b shows the comparison between the values calculated by the 10 equations along with those measured at N´ = 0.6.
Fig. 4 shows that the most accurate equation among all the equations is the S&M equation. BNS and Thomas equations give somewhat reasonable but higher values.
All the other equations give high values, especially the Tomita and SKG equations.
- The friction factors measured by Yoo at different values of NRe´ and N´ were taken as the basis for comparison. For example, Fig. 1c shows the comparison between the values calculated by the 10 equations along with those measured at N´ = 0.6753
From Fig. 1c, D&EL gives the most accurate values of friction factor compared with those measured by Clapp and K&K equations, respectively. D&M and Shenoy equations give reasonable values.
The Tomita equation gives the highest values, followed by the SKG equation, while BNS equation gives the lowest values, followed by S&M and Thomas equations.
- The friction factors measured by Szilas at different values of NRe´ and N´ were taken as the basis for comparison. For example, Fig. 1d shows the comparison between the values calculated by the 10 equations along with those measured at N´ = 0.6991.
From Fig. 1d, the first equation to give the most accurate values compared with the measured data is the BNS equation, followed by Thomas and Clapp equations. The D&EL, D&M, and Shenoy equations give reasonable values of friction factor.
Tomita, SKG, and K&K equations give the highest values, while S&M equation gives the lowest values.
*The friction factors measured by Dodge and Metzner, Shaver and Merrill, Yoo, and Szilas, discussed separately previously, will be taken henceforth as one group. Illustrating all the data are the cross plots in Fig. 2.
The friction factors that were predicted by each one of the best four equations were compared separately with all the measured data.
Evaluation based on PMD, PSD
The values of the percent mean deviation and percent standard deviation concerning each set of measured data were calculated.
PMD and PSD were calculated at each value of N´, and the different values of N´ were grouped and taken together to calculate PMD and PSD. Table 1 shows the values of PMD and PSD calculated based on considering all the measured data as one group.
For data measured by Dodge and Metzner, the best equation is the D&M equation with PSD and PMD values as 2.88 and 2.96, respectively, followed by the Clapp equation. The worst equations were SKG and Tomita.
For data measured by Shaver and Merrill, the S&M equation with PSD and PMD values as 2.89 and 1.52, respectively, represents the most accurate one, followed by the BNS equation, while Tomita and SKG equations represent the worst ones.
For data measured by Yoo, the D&EL equation gives the most accurate values with PSD and PMD values of 2.189 and –3.151, respectively. It is followed by the Clapp and Shenoy equations, while K&K, S&M, and Tomita represent the worst ones.
For data measured by Szilas, the BNS equation is the nearest, with PSD and PMD values of 0.706 and –0.687, respectively, followed by the Thomas equation, while the Tomita, K&K, and SKG equations give the lowest accurate values.
All the data show that the best equation among the published equations available in the literature is the S&M equation because it has PSD and PMD values of 8.19 and –9.69, respectively, which represent the lowest values among all the equations. The next is the BNS equation because it has PSD and PMD values as 10.99 and –14.12, respectively.
The worst equations are the Tomita equation (which has PSD and PMD values as 28.19 and 14.69, respectively) and SKG (which has PSD and PMD values as 24.36 and 30.15, respectively).
Evaluation based on % error
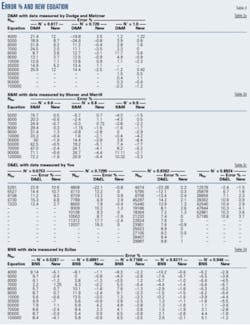
Because the best equation differs from one set of data to the other, the error % will calculate for each set of data with its own best equation as given in the parts of Table 2. These tables make clear that the D&M equation fits the data measured by Dodge and Metzner with an error % up to –34.6, while the S&M equation fits the data measured by Shaver and Merrill with an error % up to 72.2.
For the data measured by Yoo, the D&EL equation is the best with an error % up to 23.8, while the BNS equation is best for the data measured by Szilas with an error % up to 13.5.
One can observe that this equation, which is the best compared with all the measured data, has an error % up to 83.4 under some conditions. This will cause a large error in calculating the pressure loss due to friction.
Proposed equation
The previous discussion should make clear that none of the available friction-factor equations can be selected as the most accurate with respect to the individual measured sets of data. Also, if all the measured data are taken together, the most accurate equation was Shaver and Merrill, which gives PSD and PMD as 8.19 and –9.69, respectively, with an error % up to 83.4.
No equation can, therefore, be considered as a general equation to be used with all the measured data. There is a need, then, to propose a new equation to fit all the measured data with a somewhat higher degree of accuracy than the available ones.
The following discussion explains how this can be achieved.
All the measured friction-factor data, published for different values of flow behavior index and Reynolds number, were considered at their own conditions.
A regression analysis was applied to relate these three parameters to each other in which friction factor is the dependent parameter while flow behavior index and Reynolds number are the independent parameters. The proposed equation can be written as Equation 4.
This equation represents the proposed equation that can be used to determine friction factor as a function of both Reynolds number, NRe´, and flow behavior index, N´.
Confirming the validity and accuracy of the proposed friction-factor formula required comparing it with the measured data. Also, a statistical analysis was applied including PMD and PSD along with error %.
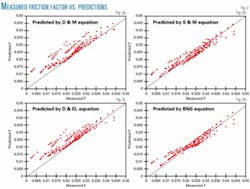
Four sets of friction-factor data are available in the literature measured by different authors. Fig. 3 shows a comparison between each set of measured friction factors with those predicted by the proposed regression equation employing the friction-factor computer program. The values predicted by the best published equations for each set of data were also plotted.
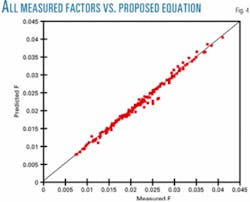
This is also shown in Fig. 4, which represents the cross plot between the predicted and all the measured friction factors. Comparing this figure with Fig. 2 reveals the better agreement of the proposed regression equation than the published ones.
To evaluate the proposed equation, we conducted a comparative study based on statistical analysis. This analysis conducted in the present research work was with PSD and PMD, which have been calculated for each value of N´, for each individual set of data, and also for all the data as one group.
Table 1gives the results of this analysis, showing that the proposed regression equation produces more reasonable values of PSD and PMD at the all values of N´. For each individual set of the measured data, the proposed equation has PSD and PMD values of 2.153 and –2.14, respectively, with the Dodge and Metzner measured data in comparison with 2.88 and 2.96 for the D&M equation.
With Shaver and Merrill measured data, the proposed equation has PSM and PMD values of 1.89 and –2.09, respectively, in comparison with 2.59 and 1.52, respectively, for the S&M equation.
With Yoo measured data, the proposed equation has PSD and PMD values of 2.596 and –2.48, respectively, compared with 2.189 and –3.151, respectively, for the D&EL equation.
With Szilas measured data, the proposed equation has PSD and PMD values of 0.741 and –0.62, respectively, compared with 0.706 and –0.689, respectively, for BNS equation.
For all the measured data as a group, the proposed regression equation gives values of PSD and PMD as 3.92 and –4.46, respectively, compared with 8.19 and –9.69 for the S&M equation that represents the best published one.
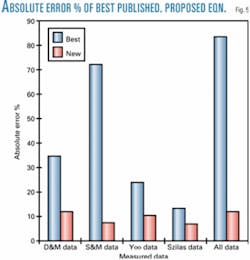
Table 2 lists the values of the error % of the proposed regression equation, and Fig. 5 shows the error % values of the best published one. Based on the error % values, the proposed regression equation has an error % up to 10.7 in comparison with 83.4 for the S&M equation that represents the best published data.
The proposed new equation, therefore, represents the most accurate to calculate friction factor when compared with other published equations. The proposed regression equation can be used to determine friction factor for any crude oil transported by pipelines.
Finally, Fig. 6 shows the proposed regression equation against flow behavior index and Reynolds number, by which one can estimate friction factor once N´ and NRe´ are known.
Evaluation using field data
The field data used here are for an Egyptian pipeline, Melieha–El-Hamrah, a 166 km, 16-in. line that transports crude oil produced by three companies: Agiba Petroleum Co., Khalda Petroleum Co., and Western Desert Petroleum Co. from Melieha to the terminal at El Hamrah. The line began operations in November 1986 when the first shipment reached El-Hamrah on Nov. 14, 1986.10
The friction factors were calculated from the measured pressure loss-flow rate data of this pipeline and compared with those predicted by the proposed friction-factor equation. Fig. 7 shows this comparison, representing the cross plot between measured and predicted values of the friction factor.
References
1. Metzner, A.B., and Reed, J.C., "Flow of Non-Newtonian Fluids—Correlation of the Laminar, Transition and Turbulent flow Regions," AIChE Journal, Vol. 1 (1955), No. 4, pp. 434-40.
2.Krantz, W.B., and Wasan, D.T., "Heat, and Mass, and Momentum Transfer Analogies for Fully Developed Turbulent Flow of Power Law Fluids in Circular Tubes," AIChE Journal, Vol. 17 (1971), No. 6, pp. 1360-66.
3.Dodge, D.W., and Metzner, A.B., "Turbulent Flow of Non-Newtonian Systems," AIChE Journal, Vol. 5 (1959), No. 2, pp. 189-203.
4.Hung, C. Y., "Turbulent Flow of non-Newtonian Fluid in Pipes and its Application to Sewage Sludge Transportation," PhD Thesis, Northwestern University, Evanston, Ill., 1994.
5.Shaver, R.G., and Merrill, E.W., "Turbulent Flow of Pseudoplastic Polymer Solutions in Straight Cylindrical Tubes," AIChE Journal, Vol. 5 (1957), No. 2, pp. 181–88.
6.Desouky, S.M., and EL-Emam, N.A., "A generalized Pipeline Design Correlation for Pseudoplastic Fluids," Journal of Canadian Petroleum Technology, Vol. 29 (1990), No. 5, pp. 48-54.
7. Yoo, S.S., "Heat Transfer and Friction Factors for non–Newtonian Fluids in Turbulent Pipe Flow," PhD Thesis, University of Illinois, 1974.
8.Szilas, A.P., Bobok, E., and Navratil, L., "Determination of Turbulent pressure losses of Non-Newtonian Oil Flow In Rough Pipes," Rheological Acta, Vol. 20 (1981), No. 5, pp. 487–96.
9.Abu-Zeid, A., "A study on the Flow Improvement of Waxy Crude Oils for Pipeline Transportation," PhD Thesis, AL-Azhar University, 1997.
10.Abdel-Kareem, E., "A Giba's Experience in Operating Meleiha EL- Hamrah Pipeline," 10th Exploration and Production Seminar, Egyptian General Petroleum Corp., Cairo, November 1990.
11.Govier, G.W., and Aziz, K., "The Flow of Complex Mixtures in Pipes," New York: Van Nostrand Reinhood Co., 1982.
12.Skelland, A.H.P., "Non-Newtonian Flow and Heat Transfer," New York: John Wiley and Sons Inc., 1967.
13.Heywood, N.I., "Pipeline Design for Non- Newtonian Fluids," Institute of Chemical Engineering Symposium, Series No. 60 (1980), pp. 33–47.
14.Garica, E.J., and Steffe, J.F., "Comparison of The Friction Factor Equations for Non-Newtonian Fluids in Pipe Flow," Journal of Food Process Engineering, Vol. 9 (1987), No. 2, pp. 93-120.
15.Khaled, S.M., "A comparative Study Among the Different Methods used for Calculating the Pressure Losses in Pipelines Transporting Non-Newtonian oils," MSc Thesis, AL-Azhar University, 1994.
16.Hanks, R.W., and Dadia, B.H., "Theoretical Analysis of the Turbulent Flow of Non-Newtonian Slurries in Pipes," AIChE Journal, Vol. 17, No. 3 (May 1971), pp. 554–57.
17.Derby, R., and Melson, J., "How to Predict the Friction Factor for Flow of Bingham Plastics," Chemical Engineering, December 1981, pp. 59-61.
18.Hawase, Y., Shenoy, A.V., and Wakabayashi, K., "Friction and Heat and Mass Transfer for Turbulent Pseudoplastic Non- Newtonian Fluids Flowing in Rough Pipes," Canadian Journal of Chemical Engineering, Vol. 72, October 1994, pp. 798-804.
The authors
N. A. El-Emam is professor of petroleum engineering at Al-Azhar University, Egypt, from which he also holds BS and MS degrees in petroleum engineering; he also holds a PhD in petroleum engineering from the Technical University of Heavy Industries, Hungary.
A. H. Kamel (ahkamel72 @yahoo.com) is an assistant lecturer in petroleum engineering at Al-Azhar University, from which he also holds BS and MS degrees in petroleum engineering. He is currently a doctoral student at the University of Oklahoma.
M. A. El-Shafei is an associate professor of petroleum engineering at Al-Azhar University, from which he also holds BS, MS, and PhD degrees in petroleum engineering.
A. M. El-Batrawy is a lecturer in petroleum engineering at Al-Azhar University, from which he also holds BS, MS, and PhD degrees in petroleum engineering.