MULTIPRODUCT OPERATIONS—1: Discrete-event simulation guides pipeline logistics
Vanina Cafaro
Diego C. Cafaro
Carlos A. Mendez
Jaime Cerda
INTEC (UNL-CONICET)
Sante Fe, Argentina
| Based on presentation to IEEE's 2010 Winter Simulation Conference, Baltimore, Dec. 5-8, 2010. |
A discrete-event simulation technique, combined with optimization tools, permits easy management of real-world pipelines operations with low computational effort.
Modeling to develop the technique used a non-traditional multi-server queuing system with a number of synchronized servers at every pipe-end and priority rules to decide which server should dispatch the entity waiting for service to the associated depot. Each priority rule can lead to a different delivery schedule, evaluated using several criteria.
Part 1 of this series discusses a novel discrete event simulation system developed on "Arena" for the detailed scheduling of a multiproduct pipeline consisting of a sequence of pipes connecting a single input station to several receiving terminals. Part 2 will conclude this discussion and apply its findings to management of a real-world multiproducts pipeline.
Background
Refined products pipelines transport a variety of oil derivatives end-to-end in successive batches. Multiproduct pipelines operate in either segregated or fungible mode. Segregated products are branded or blend-stock materials whose identity is maintained throughout transportation, and the same batch received for shipment is delivered at the destination. Fungible batches consist of generic products that meet published specifications. Shippers will receive an equivalent product matching the same product specifications, but it may not be the original lot shipped at the specified input terminal.
Pipeline scheduling
Scheduling multiproduct pipelines involves two major activities, input and delivery.
The sequence of batch injections, entering products, batch sizes, pump rates, and input terminal define the input step. Finding the optimal product input sequence and lot size aims to reduce interface costs due to product mixing or pipeline cleaning. Pipeline systems do not use separation devices and must prohibit certain sequences due to potential product contamination.
The delivery schedule specifies product batches leaving the pipeline and the amounts diverted to assigned destinations during every pumping run. This stage provides times at which pumps should be turned on-off to meet the delivery plan. Reducing the number of pipeline stoppages and pump switchings reduces energy costs and pump maintenance costs. A discrete-event simulator of multiproduct pipeline operations is a computer-aided tool for quickly generating more efficient, realistic, and robust schedules. It allows easy generation of alternative detailed schedules by changing operational criteria.
Approaches to study pipeline scheduling problems include rigorous optimization models, knowledge-based techniques, discrete-event simulation, and decomposition frameworks.1-7 Rigorous optimization methods generally consist of a single mixed-integer linear programming (MILP) or mixed-integer nonlinear programming (MINLP) mathematical formulation and are usually grouped into two classes—discrete and continuous—depending on handling of route and time domains.
Discrete formulations divide the pipeline volume into a number of single-product packs and the planning horizon into several time intervals.8-11 Most formulations generally use uniform time and volume division. Rejowski and Pinto, however, assume each pipeline segment consists of packs with equal or different prespecified volumes to account for reductions in the pipeline diameter, and the horizon length consists of time intervals of adjustable duration to allow changes in the pump injection rate.10
Neves et al. presented a decomposition approach for the planning of pipeline operations over a monthly horizon.5 The decomposition relied on a heuristic preprocessing block that accounts for demand requirements, production planning, and typical lot sizes to determine a candidate set of product sequences. The heuristic block also provides time windows for pump and delivery operations at every terminal. A continuous MILP formulation later uses the preprocessed information to determine exact start-finish times of batch input and reception.
The model includes binary variables to account for seasonal energy costs and avoid pumping operations during high-cost periods. Boschetto et al. reformulated Neves's hybrid approach with a different decomposition strategy involving three blocks:6
• Resource-allocation block determining candidate sequences of batch injections.
• Preanalysis block specifying precise volumes to be either pumped from source nodes or received in destination nodes and providing the earliest start-finish times for stripping operations at every destination node.
• Continuous-time MILP model determining the exact timing of pump and delivery operations at each node.
Most of the computational burden in multiproduct pipeline scheduling comes from three tasks:
1. Pump sequencing.
2. Batch sizing.
3. Batch allocation to receiving terminals.
Heuristically choosing them allows the remaining operational decisions to be taken in a short CPU time. The previously made heuristic-based decisions, however, greatly influence the final pipeline schedule.6
MILP-continuous optimization tools for pipeline scheduling, by contrast, do not require any decomposition and can find the optimal input schedule from a single refinery by minimizing the sum of pumping, interface, and inventory costs.12-13 Cafaro and Cerda also developed a continuous formulation for managing pipeline networks with multiple inlet points.14
Even these tools, however, just provide the set of aggregate batch stripping operations to be done during every pumping run without specifying the detailed sequence of individual cuts performed by the pipeline operator. The many ways to distribute input batches among the assigned destinations requires generating an efficient delivery schedule to accomplish optimal pipeline operation.
Simulation
Mori et al. developed a simulation model for the scheduling of injection and stripping operations in a real-world pipeline network.2 The network consists of a series of single pipes that connect multiple refineries, harbors, and distribution centers, and transport many oil derivatives. Garcia-Sanchez et al. presented a hybrid methodology combining "tabu search" and a discrete-event simulation model for addressing a real-world multiproduct pipeline scheduling problem.3 The tabu-search technique improved unsatisfactory schedules easily tested by the simulation model. Product batches divided into equally sized discrete units moved to a destination predefined when they were injected into the pipeline network.
This article introduces a discrete event simulation model for a trunk pipeline transporting refined products from a single origin to multiple distribution terminals in segregated or fungible mode. The trunk consists of a sequence of pipes, each connecting either an input to an output terminal or a pair of distribution terminals to each other.
Discrete simulation regards the pipeline as a coordinated nontraditional multiserver queuing system. The servers perform their tasks in a synchronized manner, with each one having its own queue of fixed-sized batch elements (entities). There is a server at the end of each pipe and its queue consists of the sequence of batch elements in that pipe. The length of any server queue remains fixed throughout the time horizon since every pipe should be permanently full of liquid and has a constant volume.
Solving a rigorous optimization model provides the simulator injection schedule. The simulation model considers multiple scenarios and heuristic rules to evaluate scheduling efficiency and generate alternative detailed output schedules
Example
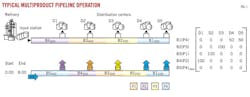
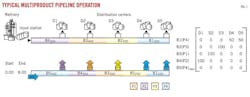
Fig. 1 represents a typical multiproduct pipeline transport system. It consists of a single refinery where oil products are injected and five distribution terminals at different sites along the pipeline.
The first line in Fig. 1 depicts the location of every batch inside the pipeline (linefill) at the start of the time horizon, four batches (B4(P2)-B3(P1)-B2(P3)-B1(P4)) with 400, 400, 350, and 350 volumetric units of product, respectively. The next line in Fig. 1 shows the pipeline contents after completing the first injection. It consists of 400 units of product P4, pumped from 0.00 hr to 8.00 hr (represented by a right arrow) into the new batch B5(P4)new. A series of up arrows also shows associated product deliveries to every terminal.
Due to liquid incompressibility, the volume of product injected in the pipeline origin equals the sum of product deliveries to receiving depots, i.e., 400 = 100 + 100 + 100 + 50 + 50. The optimization model proposed by Cafaro and Cerda not only generates an efficient input schedule but also provides the set of stripping volumes to be transferred during every batch injection.12-13
Hierarchical solution
Solving the scheduling problem hierarchically requires two stages, the first one generating the input schedule through the optimization module and the second developing a detailed delivery schedule based on the information provided by optimization. An efficient discrete event simulation system developed on Arena both validates the pipeline schedule provided by the optimization module and generates the detailed output schedule.15 The model allows visualizing pipeline operations through an animation interface showing pipeline system dynamics over time.
The simulator uses the set of batches to be stripped and the related number of entities to be delivered to the distribution terminals while performing a pumping run as input data, the so-called terminal-batch assignment matrix (Qko(i,j)) whose element qko(i,j) represents the product demand at terminal j covered by batch i during pumping run k. The terminal-batch assignment matrix Qk appears at the right side of Fig. 1.
The simulator, however, must determine the detailed order of execution of stripping operations. Some operations could be done in two or more non-consecutive steps, requiring further work before fully developing the pipeline delivery schedule.
Since a pumping run is divided into a sequence of events, and batches flowing through the line are discrete entities, the matrix Qko(i,j) can easily derive the possible destinations for each entity and occurrence of each event. When a new input event occurs, therefore, each pipe server knows if the first entity on its queue is eligible for being transferred to the associated terminal. The entity should otherwise move to the next pipe.
If two or more servers can dispatch the leading entry to their output terminals to meet unsatisfied demand, the simulation model should decide, based on priority rules, which one is chosen. Simulating the pipeline schedule provided by the optimization package requires delivering the specified stripping volumes for every run, k, and satisfying terminal demands, qko(i,j).
The simulation model should update unsatisfied demands, qk(i,j), at every terminal—initially equal to qko(i,j)—for each time event. If qk(i,j) drops to zero, such a terminal, j, can no longer receive an entity from batch i. Reaching null for all unsatisfied demands qk(i,j), generates the output schedule for run k.
Previous work assumed the destination for each entity was already given by the optimization package.2-3 This article's approach provides some capabilities to the proposed simulation model for selecting the route to be followed by every entity based on three key elements:
• The assignment matrix, Qko(i,j), for every run, k.
• The batch to which each entity belongs.
• A set of priority rules selecting both the leaving entity and the receiving terminal (if several cut operations are eligible for execution).
Changing the priority rules can generate different pipeline output schedules. The simulation model can also consider operational details like loading and unloading individual tanks at input and distribution terminals, instead of handling them in aggregate. These abilities allow the simulation model both to track the evolution of inventory in every individual tank over time and address pipeline stoppages due to high-cost peak periods.
Problem statement
Effectively stating the problem to be overcome in product scheduling requires defining:
• A multiproduct pipeline connecting an oil refinery to several distribution terminals.
• Number, type of products to be transported through the pipeline.
• Set of product batches to be pumped (input schedule).
• Associated set of stripping volumes to be transferred during each batch injection (terminal-batch assignment matrix, Qko(i,j)).
• Scheduled production runs to be loaded into the tanks of the input station.
• Initial pipeline conditions (sequence of batches inside the line at t = 0 and their sizes).
• Initial inventory level of every product in terminal tanks.
• Hourly product demand profile at the distribution centers.
• Constant product pumping rate.
• Time-horizon length.
Generating the detailed delivery schedule requires explicitly defining:
• Sequence of batch portions to be pumped into the pipeline.
• Size of every portion and starting-end times of related injections.
• Amount, type of product delivered to a storage tank from a batch arriving at an output terminal for each injection.
• Time at which a batch portion has been completely loaded in the terminal tank.
• Product inventory management at the delivery terminals based on hourly discharged product lots and client demands.
Major assumptions
Developing a pragmatic representation of the real-world problem requires next considering assumptions in the discrete-event simulation model:
• A unidirectional pipeline connecting a single refinery to multiple distribution terminals is considered. The model, however, can be extended to manage network topologies.
• The pipeline is always full of liquid products and operates either in segregated or fungible mode. In the latter mode, a single batch can have many destinations.
• Batches of products are injected into the pipe one after the other, with no physical barrier between them.
• Interface, contamination loss between a particular pair of refined products is a known constant.
• Liquid incompressibility requires every time an element of a batch is injected that one and only one entity already in the line be simultaneously transferred from the pipeline to a single receiving terminal.
• Every batch portion is pumped at a fixed flow rate.
• Distribution centers are tank farms with dedicated storage units of known capacity for each product.
• One terminal tank, at most, is connected to the pipeline at any time event and the setup time for switching from one tank to another is negligible.
• Refinery production schedules are developed in advace. Scheduled start-end times and rates of incoming product flows to storage tanks at the input station are problem data.
• Daily client demands are expressed as deterministic data on an hourly basis.
Objective function
The sequence in which product deliveries to distribution terminals are accomplished greatly affects operational costs. Pipeline stoppages are particularly expensive and should be avoided.4 A pipe stoppage occurs whenever a delivery at a terminal is interrupted forcing a different stripping operation to start at an upstream point. Stoppages cause interruption of the flow in the pipeline segment connecting the activated and the deactivated output nodes, and consequent shutdown of several pump stations.
The main cost of stoppage comes from the lost energy of fluid momentum, since the stopped flow itself will move again to resupply downstream destinations. Maintenance costs also increase with the number of stoppages, with the time between pump repairs strongly dependent on the number of shutdowns.
Measuring the quality of the resulting output schedule requires defining the so-called accumulated idle volume. Adding the product volumes in idle pipes across the complete horizon computes this variable. The accumulated idle volume together with the total number of cut operations required to meet the specified terminal demands are the two performance measures used to compare alternative pipeline output schedules.
Model structure
A refined products pipeline network consists of an input station, a set of receiving terminals, and pipes connecting the tank storage facilities. Oil products arriving at the input station from neighboring refineries remain in tanks temporarily until injection runs transfer material from the input station tanks to the pipeline system. Specifying the type of product injected, the batch size, and the expected pumping rate also takes place at this point, each injection run creating a new batch to be pumped into the line from the input station.
Injection run sequence determines input schedule. Introducing a new product batch forces preceding batches forward, and another product batch already in transit is simultaneously transferred from the pipeline to a receiving terminal.
A list of time events, each one representing the injection time of a single element into the system, provides the basis for simulation of pipeline operations. The simulation model scheduler block generates the event list, accounting for the input schedule. The optimization approach permits generating the input schedule for the following month, showing the sequence of batches to be injected and the batch attributes (product, volume, pump rate, and start pumping time).12-13
Handling product batches in a discretized manner requires expressing their volumes as a number of small, equal-size batch elements called entities. Entity attributes come from the batch to which it belongs. Linefill similarly consists of a sequence of entities defining the queue of the pipe server. Each event represents the pumping of a single entity into the line. The state of the pipeline system, therefore, changes only when an event is accomplished.
Each time an elementary pumping operation occurs at the input station (i.e., at the inlet of the first pipe) a new entity enters the first-server queue, and another entity at the exit of one of the pipes should be dispatched to the corresponding receiving terminal. The set of servers should jointly decide which one will dispatch the first entity on its queue to the associated distribution terminal (dispatching server). The servers will also determine which servers should transfer the entity in transit to the next pipe (servers upstream of the dispatching server) and which will remain idle because there are no new arrivals (servers downstream of the dispatching server).
A pipe server, in other words, can take three different actions whenever an event is accomplished:
• Remain idle, because there is no product arrival to its queue.
• Transfer the first entity waiting for service to the next pipe.
• Deliver the first entity on the queue to its receiving terminal.
A new entity arrival to the server queue triggers the second two actions, so only a single distribution terminal will be active on every pumping event.
Entity volume (a user choice) and the pumping rate for the current injection determine the service time of an entity. After the servers perform their jobs, the simulation clock advances to the next event time. Delays can arise if the selected distribution terminal lacks sufficient storage capacity to receive the departure entity, leading to disrupted pipeline operations.
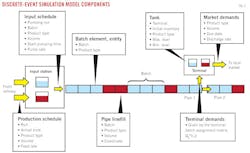
Simulation blocks
The model structure involves three blocks, each representing a main component of the pipeline system: the input station, the receiving terminals, and the pipes. Fig. 2 shows the model blocks together with key simulation elements, such as entities (batch elements), and resources.
References
1. Sasikumar, M., Prakash, P.R., Patil, S.M., and Ramani, S., "Pipes: A heuristic search model for pipeline schedule generation," Knowledge-Based Systems, Vol. 10, pp. 169-75, 1997.
2. Mori, F.M., Luders, R., Arruda, L.V.R., Yamamoto, L., Bonacin, M.V., Polli, H.L., Aires, M.C., and Bernardo, L.F.J., "Simulating the operational scheduling of a real-world pipeline network," Computer Aided Chemical Engineering, Vol. 24, pp. 691-96, 2007.
3. Garcia-Sanchez, A., Arreche, L.M., and Ortega-Mier, M., "Combining simulation and tabu search for oil-derivatives pipeline scheduling," Studies in Computational Intelligence, Vol. 128, pp. 301-25, 2008.
4. Hane, C.A., and Ratliff, H.D., "Sequencing inputs to multi-commodity pipelines," Annals of Operations Research, Vol. 57, pp. 73-101, 1995.
5. Neves Jr., F., Magatao, L., Stebel, S.L., Boschetto, S.N., Felizari, L.C., Czaikowski, D.I., Rocha, R., and Ribas, P.C., "An Efficient Approach to the Operational Scheduling of a Real-World Pipeline Network," Computer Aided Chemical Engineering, Vol. 24, pp. 697-702, 2007.
6. Boschetto, S.N., Felizari, L.C., Yamamoto, L., Magatao, L., Stebel, S.L., Neves Jr., F., Arruda, L.V.R., Luders, R., Ribas, P.C., and Bernardo, L.F.J., "An Integrated Framework for Operational Scheduling of a Real-World Pipeline Network," Computer Aided Chemical Engineering, Vol. 25, pp. 259-64, 2008.
7. Moura, A.V., de Souza, C.C., Cire, A.A., and Lopez, T.M., "Planning and Scheduling the Operation of a Very Large Oil Pipeline Network," Principles and Practice of Constraint Programming, Lecture Notes in Computer Science, Vol. 5202, pp. 36-51. DOI: 10.1007/978-3-540-85958-1, 2008.
8. Magatao, L., Arruda, L.V.R., and Neves Jr., F., "Mixed integer programming approach for scheduling commodities in a pipeline," Computers & Chemical Engineering, Vol. 28, pp. 171-85, 2004.
9. Zyngier, D., and Kelly, J.D., "Multi-product inventory logistics modeling in the process industries," in Chaovalitwongse, W., Furman, K.C., and Pardalos, P.M. (Eds.), Optimization and logistics challenges in the enterprise. Springer optimization and its applications, pp. 61-95, New York: Springer, 2009.
10 Rejowski, R., and Pinto, J.M., "A novel continuous time representation for the scheduling of pipeline systems with pumping yield rate constraints," Computers and Chemical Engineering, Vol. 32, pp. 1,042-66, 2008.
11. Herran, A., de la Cruz, J.M., and de Andres, B., 2010, "A mathematical model for planning transportation of multiple petroleum products in a multi-pipeline system," Computers and Chemical Engineering, Vol. 34, pp. 401-13, 2010.
12. Cafaro, D.C., and Cerda, J., "Optimal scheduling of mulitiproduc pipeline system using a non-discrete MILP formulation," Computers and Chemical Engineering, Vol. 28, pp. 2,053-68, 2004.
13. Cafaro, D.C., and Cerda, J., "Dynamic scheduling of multiproduct pipelines with multiple delivery due dates," Computers and Chemical Engineering, Vol. 32, pp. 728-53, 2008.
14. Cafaro, D.C., and Cerda, J., "Optimal Scheduling of Refined Products Pipelines with Multiple Sources," Industrial & Engineering Chemistry Research, Vol. 48, pp. 6,675-89, 2009.
15. Kelton, W.D., Sadowski, R.P., and Sturrock, D.T., Simulation with ARENA, Fourth Ed., New York: McGraw-Hill, 2007.
The authors
More Oil & Gas Journal Current Issue Articles
More Oil & Gas Journal Archives Issue Articles
View Oil and Gas Articles on PennEnergy.com