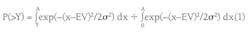Dependent on dependence: Are economic calculations of expected hydrocarbon accumulations worthwhile?
J.A. MacKay
Rose & Associates
Houston
Ian Lerche
Martin Luther University
Halle-Wittenberg, Germany
This article is concerned with showing that the dependence of probable success between two reservoirs has far-reaching consequences for the expected value, volatility, and cumulative probability of anticipated hydrocarbon reserves.
In particular, varying the allowed probability for the dependent reservoir is shown to not influence either the expected project value or the standard deviation around the expected value. The result is that the cumulative probability of obtaining a hydrocarbon reserve in excess of a fixed amount is also not influenced by the dependence probability chosen and behaves as though the two reservoirs were totally independent of each other.
This result indicates that a corporation could spend an inordinate amount of time and money attempting to resolve an irresolvable (or at least noncritical) problem.
Introduction
Making quantitative assessments, ahead of drilling, of the likely amount of hydrocarbons one expects to find in a reservoir is one of the mainstays of economic projections for oil exploration, and one that colors to a large extent precisely what a corporation should do to ensure financial health.
Indeed, precisely that sort of effort has been the dominant theme of two volumes1 2 treating with such problems. The basic concerns of risk and economic worth have been one of the mainstays of hydrocarbon exploration for over half a century as is ably recorded in many works.3 11
And yet it is to be doubted that all possible configurations of exploration assessment have been investigated to date. Perhaps one of the lacunae in such treatments has been the unresolved issue of what happens with assessments when there is dependence between likely reservoirs in terms of their probabilities of being successful in estimating hydrocarbon reserves.
Note that dependence is different than correlation; when dealing with a correlated assessment of reservoir success chances one is usually in the situation where if the probability is high or low of one reservoir being successful then the high (low) probability of a second reservoir being hydrocarbon bearing is related to the probability of the first reservoir.
In the case of dependence the argument is different. Here one has to deal with some form of constraint so that there is a relationship between the two reservoirs either in terms of a fixed relationship, a so-called holonomic constraint (for instance so that a given number of barrels of oil is divided between the two reservoirs, representing a closed system, or when a finite number of barrels can be lost to the reservoirs) or in terms of a range of values, a so-called nonholonomic constraint (for instance, the probability of the second reservoir being successful (or unsuccessful) given that the first was successful (or unsuccessful) should not exceed a predetermined value).
Note that a nonholonomic probability constraint differs from an holonomic constraint because one refers to the probability of success and the other refers to the amount likely to be found. Thus if one reservoir is likely to contain a large hydrocarbon accumulation then one can either take it that a second reservoir will likely also contain a large supply or that there is a high chance of success with the second reservoir irrespective of the amount to be found.
Such dependence arguments have also had a long history in the hydrocarbon exploration arena and modern interpretations, with many references to earlier works, can be found in Rose,10 Bickel and Smith,12 Lerche, and Mackay,2 and Bickel, Smith, and Meyer.13
In any event the quantitative evaluation of a dependency has far-reaching repercussions for attempts to assess the exploration potential. It is this fact that the present article will illustrate with a simple example.
More complex dependency situations than that to be discussed in the next section of the article will, presumably, just enhance the unexpected patterns of behavior uncovered with the simple illustration.
Dependency for a two-reservoir problem
Quantitative evaluation
Consider a system of two potential reservoirs in which, ahead of drilling, it has been estimated that reservoir A could have 10 million bbl of reserves and reservoir B could have 30 million bbl.
If one were to treat the two reservoirs as independent entities and assign to reservoir A the success probability (Pa) 20% and to reservoir B the success probability (Pb) 10% then the expected value (EV) of the two reservoir system is 5 million bbl, being composed of EV = Pa*A + Pb*B, where A = 10 million bbl and B = 30 million bbl (Fig. 1).
Now consider however that there is dependence between reservoir B and reservoir A. This dependence can arise either because the estimate of hydrocarbon reserves in reservoir B depends on the estimate made for the reserves in reservoir A or, and most often the case, such a dependence can arise because one assesses the probability of success for reservoir B to be a consequence of both the probability of success of reservoir A ahead of the drill as well as the resulting outcome of drilling reservoir A first.
Such a situation can be of value in play and portfolio evaluation because one has a local risk tied to whatever is known or surmised about each reservoir plus, of course, the shared risk of the two reservoirs that is a consequence of the assessed regional geology and assessed hydrocarbon flow within a larger domain encompassing the reservoirs.
In addition, based on the total assessment of potential reserves in both reservoirs that was made ahead of drilling either reservoir, one considers that the total probability of success of reservoir B shall not change from the independent estimate made of 10% no matter what the result of drilling reservoir A would yield. An alternative is to specify a maximum success probability the corporation will accept as "reasonable."
In either event the constraint imposed is nonholonomic and with far-reaching consequences. The point being made is most easily illustrated with the simple case of the restraint at 10%.
In that case one has a very different procedure to use to estimate the expected value of the two reservoir system. Because there is the chance that A may be unsuccessful (successful) but B may still be either unsuccessful or successful one has now to include the provision that one will still drill reservoir A and reservoir B.
Fig. 2 sketches the various outcomes with assigned probabilities of each outcome. However in this case the constraint that whatever one does there is a corporate limit of 10% imposed that reservoir B will be successful means that one is not free to choose the subordinate probabilities for C, D, E, and F independently—there is a dependence. Denote by Pc, Pd, Pe, and Pf the relevant probabilities associated with the marked domains in Fig. 2.
What is now the case is that the constraint of a total 10% probability for reservoir B implies Pa*Pc + Pd*Pe =Pb = 10%. Now if Pe were to be zero then Pa*Pc = Pb so that Pc = 100*min(1, Pb/Pa) %, which is 50% for the values given for Pa. This situation is labeled positive dependency because Pe is chosen zero and so Pc is positively dependent on the value chosen for Pa.
On the other hand if Pc is chosen zero then Pe = 100*min(1, Pb/Pd) %, which is 13% for the values reported in Fig. 2. This situation is labeled negative dependency because now Pc is chosen zero.
The point about this situation is that Pc can have any value in between 50%>Pc>0%. When one assigns any value whatsoever to Pc in the allowed range then the expected value of the Fig. 2 decision tree diagram is independent of the assigned value for Pc and is precisely the expected value for the situation where A and B are treated as independent reservoirs. Not only that, but the standard deviation around the expected value is also independent of the value chosen for Pc within the limiting range and is 9.2 million bbl, in agreement with the situation where A and B are taken to be independent when the standard deviation is also 9.2 million bbl.
One aspect of this independence is that one can provide immediately a cumulative probability curve of the chances of exceeding a fixed value, and this curve does not change as the probability dependence is varied. Fig. 2 shows the cumulative probability curve for the parameters of Fig. 1.
A corollary is that if one were to replace Pb in the above argument by any value whatsoever then one would again obtain a range of values for Pc for which there is no change in the expected value or the standard deviation, although the expected value would then be different than for the situation where A and B are treated as independent. In other words, there is a large class of situations for which dependency (either negative or positive) allows no distinction between possible outcomes—this general result has far-reaching implications for a corporation as is discussed below.
A measure of the trustworthiness of the expected value is the volatility, defined as standard deviation divided by expected value. If the volatility is much less than unity then the expected value represents a good assessment of likely worth whereas a volatility much larger than unity informs that the expected value has a large uncertainty and less confidence should be placed in the expected value as a good representation of the worth. For the values reported in Fig. 1 (A and B treated as independent) the volatility is 1.96 while in the dependent case shown in Fig. 2 the corresponding volatility is also 1.96 because both the expected value and the standard deviation are identical.
One of the more useful measures of worth is the cumulative probability, P (>Y), of obtaining a worth exceeding a chosen amount Y. However, one must also ensure that one does not violate the maximum allowed value, obtained when all probabilities are maximized and for which the total available reserves are then 40 million bbl for the example given in Figs. 1 and 2. Hence one writes:
where EV is the expected value and σ is the standard deviation: A is the maximum amount of reserves (for the example A = 40 million bbl).
Equation (1) is valid for A>Y>0 so that one has a valid descriptor of the influence of uncertainty on the anticipated worth of the situation including the dependence. Fig. 3 shows the corresponding cumulative probability and value (in million barrels).
Three markers considered of worth in the oil industry are P10, P50, and P90, which are the values of Y corresponding to 10%, 50%, and 90% cumulative probability of greater than the defined value, respectively.
For the example of Fig. 2 these marker values are 28, 11, and 2.2 million bbl, respectively. The three values provide a corporation with an assessment of worth in the sense that a P50 of 11 million bbl indicates there is a 50-50 chance of either more or less than 11 million bbl, while the ratio of |(P90-P50)/(P50-P10)| provides an indication of the anticipated likely dynamic range possible and takes on the value 0.52 indicating there is about a 2:1 bias around the P50 value for assessing likely value, as could also have been obtained directly from the differences in the marker values around the P50 value(11 million bbl vs. 9 million bbl).
It is unlikely that one will obtain less than 2.2 million bbl but equally unlikely one will obtain more than 28 million bbl—estimated at the 10% and 90% probability values.
In addition, because the expected value and the standard deviation are identical for both cases then the cumulative probability curve shown in Fig. 2 is also applicable to the case where both A and B are taken to be independent.
Economic considerations
In deciding whether to undertake a project a corporation usually makes an assessment first of likely reserves and then undertakes an economic valuation based on costs of drilling, chances of success, selling price of product, and so on. A corporation will usually run through a series of scenarios changing the conditions of probabilities, reserves anticipated, etc.
But now with the above simple two-reservoir calculation, one has the situation where one has precisely the same expected value and precisely the same standard deviation around the expected value no matter how one changes the probability—within the dependency limits given. Thus there is no way a corporation can now know what probability to assign to reservoir B to assess a change in economic worth.
This ambiguity means that there is no clear-cut decision available to a corporation. It also means that groups within a corporation can promote high probabilities of success with low resource potential whereas equally valid are low probabilities of success with high resource potential—based on either positive or negative dependence.
There is no other measure available because the expected value and standard deviation are the same for all such situations, a true quandary for a corporation considering the worth of undertaking a project.
As also pointed out, it does not help to change the dependence condition (i.e., to change the condition to a fixed value other than Pb) because all one does by so doing is to change the allowed range of probabilities without changing the essential fact that the EV and standard deviation are again fixed, independent of the value chosen.
Even more disconcerting is that the example given is a simple decision tree determination. For more complex decision trees (usually the rule in corporate decision making) there is always some sort of dependence of one outcome on others. What is unknown is how one can sort out the situations where variables do change as one adjusts parameters from those situations where only partial variation occurs because of lack of dependence; to date there would not seem to be available any general method for so doing. This problem is an outstanding concern.
Discussion and conclusion
Perhaps the central issue here is that if the expected value and variance do not chance with dependency such means that dependency in a portfolio is also not important in the long run.
If one drills 20 wells all dependent then they will all succeed or fail and have an EV of $100 million or, if independent, some will succeed and others fail but the EV is still $100 million. The only difference might be how quickly the two situations regress to that mean value of $100 million/year average. Since the expected volatility is the same, both situations will regress at the same rate (after 20 years one will make the same profit in the long run).
However, what the simple model discussed here shows is that corporations that really want to include dependence will spend more money trying to resolve situations that are intrinsically irresolvable and cannot be distinguished from independent cases—a somewhat less than satisfactory situation.
The problem is to find a general procedure that will allow one to identify such dependent situations and when they might be worthwhile to pursue relative to treating the exploration assessment from a completely independent viewpoint. This problem is an open domain at the time of writing.
The real economic issue here is the lack of ability to get value from information. The situation considered is where one takes it that a corporation always drills both prospects regardless of the outcome of A. As such the expected value does not change, but if the company could decide to stop because of the known dependence then the expected value will change. So if one is going to drill both reservoirs regardless, do not estimate dependence. If one might stop after drilling prospect A then it is important to know this fact.
Apart from the unanticipated behavior uncovered here with dependence, there are two further aspects to the basic problem. First is the question of the financial expected value, uncertainty, and cumulative probability of making a profit under a situation where dependence is present; second is the problem of correlation between reservoir amounts, so that if one reservoir has a high (low) reserve estimate then the second reservoir can have either a high (low) reserve estimate if the reservoirs are considered positively correlated or can have a low (high) reserve estimate if the reservoirs are negatively correlated. These two aspects have not been addressed here because interest was focused on showing the dependence behavior with as clean and simple an illustration as possible. These deferred problems will be addressed elsewhere.
References
1. Lerche, I., and MacKay, J.A., "Economic Risk in Hydrocarbon Exploration," Academic Press, 1999, 403 pp.
2. Lerche, I., and MacKay, J.A., "Faults, Flow, Finance and Pressure in Exploration Assessments," MultiScience Press, 2007, 328 pp.
3. Megill, R.E., "Exploration Economics," Petroleum Publishing Co., Tulsa, 1971.
4. Megill, R.E., "An Introduction to Risk Analysis," Petroleum Publishing Co., Tulsa, 1977.
5. Newendorp, P.D., and Root, P.J., "Risk Analysis in Drilling Investment Decisions," J. Pet. Tech., Vol. 20, 1968, pp. 579-85.
6. Newendorp, P.D., "Decision Analysis for Petroleum Exploration," Petroleum Publishing Co., Tulsa, 1975.
7. Nind, T.E.W., "Profitability of Oilfield Projects," Southam-MacLean's Oil/Gas World, 1959, p. 14.
8. Nind, T.E.W., "Principles of Oil Well Production," McGraw-Hill Book Co., New York, 1981, 391 pp.
9. Rose, P.R., "Dealing with Risk and Uncertainty in Exploration: How can we Improve?," AAPG Bull., Vol. 71, 1987, pp. 1-16.
10. Rose, P.R., "Chance of success and its use in petroleum exploration," in R. Steinmetz, ed., "The Business of Petroleum Exploration," AAPG Treatise of Petroleum Geology: Handbook of Petroleum Geology, 1992, pp. 71-86.
11. Rose, P.R., "Implementing Risk Analysis in Exploration Organizations: What Works? What Doesn't?," notes distributed at the AAPG meeting, 1994.
12. Bickel, J.E., and Smith, J.E., "Optimal Sequential Exploration: A Binary Learning Model," Decision Analysis, Vol. 3, 2006, pp. 16-32.
13. Bickel, J.E., Smith, J.E., and Meyer, J.L., "Modeling Dependence Among Geologic Risks in Sequential Exploration Decisions," SPE Reservoir Evaluation and Engineering, Vol. 3, 2008, pp. 233-51.
The authors
More Oil & Gas Journal Current Issue Articles
More Oil & Gas Journal Archives Issue Articles
View Oil and Gas Articles on PennEnergy.com